WordPressのMathJax-LaTeXの使い方です。 今後も追記していきます。
プラグインのインストール
ワードプレスでMathJaxを使うには、まずMathJax-LaTeXのプラグインをインストールする必要があります。
1-1:右のメニューから『プラグイン』を選択。
1-2:下の様に『新規追加』のボタンを押し、
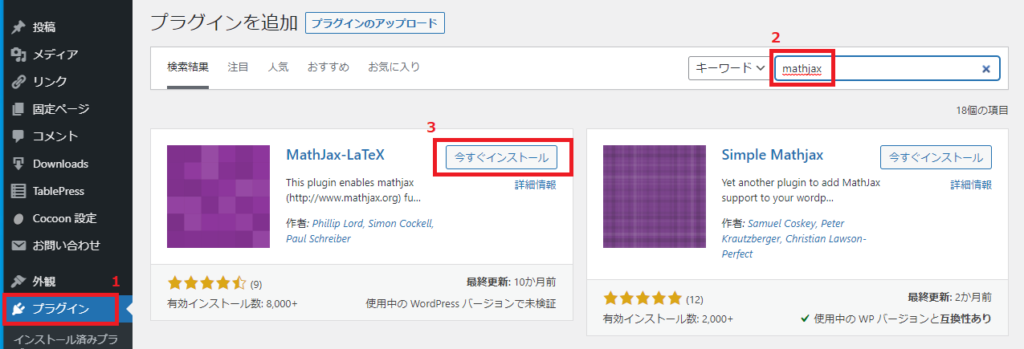
2: キーワードに『mathjax』と入力する。
3: 表示されたプラグインから、MathJax-LaTeXの『今すぐインストール』を押す。
4: インストールが終わったら、『プラグイン』を再度押す。
インストールしたプラグインの一覧のぺージでMathJax-LaTeXを『有効』にする。
MathJax-LaTexの使用宣言
ぺージの最初でも、途中でも [mathjax]というショートコードだけをブロックに記述する。
下はショートコード記述例。 タイトルの部分以外に、[mathjax]と記述。 ショートコードなので実際には表示されません。 (注意:タイトル部(H1)への[mathjax]の記述は動作しませんでした。)

記述方法(基本)
数式を \( と \ )でくくる。(半角文字のみ)(¥は半角バックスラッシュの事。 テーマ設定によっては、半角バックスラッシュが半角円マークに表示される事があります。)
下のように記述すると、
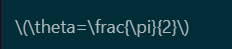
この様に表示される。 でも分数が一行に表示されるので表示が小さいのです。 見やすく大きく表示するには、次の『見やすい表示方法』の様にすると見やすくなります。
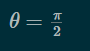
\(\theta\)や分数や\(\pi\)記号等の特殊文字を表示する時は、半角バックスラッシュの後にthetaやfracやpi等と表記すると表示されます。 式の表記一覧やギリシャ文字一覧参照
見やすい表示方法
\( の後に、\displaystyle を付けると、縦長の記号は1行内に収まる小さな形状でなく、縦長サイズで表示されます。(ワードプレスで、inlineでなくdisplayに設定しましたが縦長表示されませんでした。 しかし、\displaystyleを付けると、ちゃんと縦長表示になりました。)

この様に、縦長になって表示されます。
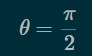
式表記一覧表
下の表の記述方法に書かれた内容の前後に、\( と \ )を付ける。(半角を使用する事。テーマやCSS設定などで円マークで表示される事もありますが、半角バックスラッシュのキーで入力します。)
| 式 | Tips | 記述方法 |
|---|---|---|
| \(2*x+2x-2\times 5 \) \(\div\) | \times \div | 2*x+2x-2\times 5 \div |
| \(x^2 + 3x-y\) | x^2 + 3x-y | |
| \((x+3)(2y-5)\) | (x+3)(2y-5) | |
| \(\{(x+3)(2y-5)+x^2\}\) | \{ \} | \{(x+3)(2y-5)+x^2\} |
| \(x\cdot x=x^2\) | \cdot | x\cdot x=x^2 |
| \(x1+x2+\cdots+xn\) | \cdots | x1+x2+\cdots+xn |
| \(x_1+x_2+\cdots+x_n\) | _ | x_1+x_2+\cdots+x_n |
| \(X_1, X_2,\ldots ,X_n\) | \ldots | X_1, X_2,\ldots ,X_n |
| \(12x\div{y}\) | \div{値} | 12x\div21y |
| \(\displaystyle\frac{12x}{21y}\) | \frac{ 分子 }{ 分母 } | \(\displaystyle \frac{12x}{21y}\) |
| \(x^{2n+1}\) | {数式} | x^{2n+1} |
| \(x^{(3n+1)^{p}}\) | {p} | (x^{(3n+1)^{p}} |
| \(\sqrt{a} + \sqrt{b} + \sqrt{c} + \sqrt{d}\) | \sqrt{数式} | \sqrt{a} + \sqrt{b} + \sqrt{c} + \sqrt{d} |
| \(\sqrt{\mathstrut a} + \sqrt{\mathstrut b} + \sqrt{\mathstrut c} + \sqrt{\mathstrut d}\) | \mathstrut 修飾記号の高さ合わせる | \sqrt{\mathstrut a} + \sqrt{\mathstrut b} + \sqrt{\mathstrut c} + \sqrt{\mathstrut d} |
| \(\sqrt[3]{4x}\) | \sqrt[ 乗根 ]{ 数式 } | \sqrt[3]{4x} |
| \(x=\pm 5\) | \pm | x=\pm 5 |
| \(\|a\|\) | \| | \|a\| |
| \(\displaystyle\left(\frac{1}{6}\right)\) | \left( 数式 \right) | \displaystyle\left(\frac{1}{6}\right) |
| \(\displaystyle\left[\frac{2}{5}x^2-2y\right]\) | \left[ 数式 \right] | \displaystyle\left[\frac{2}{5}x^2-2y\right] |
| \(\displaystyle\left\{\frac{2}{5}x^2-2y\right\}\) | \left\{ 数式 \right\} *注意:\ が2度必要 | \displaystyle\left\{\frac{2}{5}x^2-2y\right\} |
| \(\displaystyle\left|\frac{2}{5}x^2-2y\right|\) | \left| 数式 \right| | \displaystyle\left|\frac{2}{5}x^2-2y\right| |
| \(\Biggl( \biggl(\Bigl(\bigl(a\bigr)\Bigr)\biggr)\Biggr) \) \(\Biggl[ \biggl[\Bigl[\bigl[a\bigr]\Bigr]\biggr]\Biggr] \) \(\Biggl\{ \biggl\{\Bigl\{\bigl\{a\bigr\}\Bigr\}\biggr\}\Biggr\} \) \(\Biggl| \biggl|\Bigl|\bigl|a\bigr|\Bigr|\biggr|\Biggr| \) \(\Biggl\| \biggl\|\Bigl\|\bigl\|a\bigr\|\Bigr\|\biggr\|\Biggr\| \) | \Biggl. \Biggr ---(), [], |, \{ \biggl, \biggr \Bigl, \Bigr \bigl, \bigr | \Biggl( \biggl(\Bigl(\bigl(a\bigr)\Bigr)\biggr)\Biggr) \Biggl[ \biggl[\Bigl[\bigl[a\bigr]\Bigr]\biggr]\Biggr] \Biggl\{ \biggl\{\Bigl\{\bigl\{a\bigr\}\Bigr\}\biggr\}\Biggr\} \Biggl| \biggl|\Bigl|\bigl|a\bigr|\Bigr|\biggr|\Biggr| \Biggl\| \biggl\|\Bigl\|\bigl\|a\bigr\|\Bigr\|\biggr\|\Biggr\| |
| \(x < 0, y > 1\) \(x < 0, \! y > 1\) \(x < 0, \, y > 1\) \(x < 0, \: y > 1\) \(x < 0, \; y > 1\) | 空白を無視される。 \! =>余白を圧縮 \, \: \; | x < 0, y > 1 x < 0, \! y > 1 x < 0, \, y > 1 x < 0, \: y > 1 x < 0, \; y > 1 |
| \(x < 0, \quad y > 1\) | \quad | x < 0, \quad y > 1 |
| \(x < 0, \qquad y > 1\) | \qquad | x < 0, \qquad y > 1 |
| \(x < 0, \hspace{40pt} y > 1\) | \hspace{空白大きさ} pt,pc,mm,cm | x < 0, \hspace{40pt} y > 1 |
| \(x < 0, \enspace\enspace y > 1\) | \enspace | x < 0, \enspace\enspace y > 1 *1文字分 |
| \(x < 0, \\[30pt]\\ y > 1\) | \\[改行スペース] | x < 0, \\[30pt]\\ y > 1 *注意:鍵括弧でなく[ ]を使う。 |
| \(\text{≦}, \text{≧}\) | \text{≦} \text{≧} | \text{≦}, \text{≧} |
| \(\leq,\geq\) | \leq,\geq | \leq,\geq |
| \(\ll, \gg \) | \ll, \gg | \ll, \gg |
| \( \neq \) | \neq | \neq |
| \(\unicode{x2252}\) | \unicode{番号} | \unicode{x2252} |
| \( \approx \) | \approx | \approx |
| \(\fallingdotseq\) \( \risingdotseq\) \(\leqq\) \(\geqq\) \(\veebar\) \(\triangleq\) | \fallingdotseq \risingdotseq \leqq \geqq \veebar \triangleq | \fallingdotseq \risingdotseq \leqq \geqq \veebar \triangleq *ver3.5で確認。2.7表示ではせず。 |
| \(\simeq \) | \simeq | \simeq |
| \( \sim \) | \sim | \sim |
| \(\backsim\) | \backsim | \backsim *ver3.5で確認。2.7表示ではせず。 |
| \(\unicode[sans-serif]{x223D}\) | \unicode[フォント名]{番号} | \unicode[sans-serif]{x223D} |
| \(\equiv\) | \equiv | \equiv |
| \(\unicode{x225C}\) \(\unicode{x225D}\) \(\unicode{x2254}\) \(\unicode{x2255}\) | 全て『左辺を右辺で定義する』の意味 | \unicode{x225C} \unicode{x225D} \unicode{x2254} \unicode{x2255} |
| \(\unicode{x2262}\) | \unicode{番号} | \unicode{x2262} |
| \(\infty \) | \infty | \infty |
| \(\propto\) | \propto | \propto |
| \( /\!/ \) | /\!/ | /\!/ |
| \(\angle{ABC}\) | \angle | \angle{ABC} |
| \(45\text{°}\) \(45^{\circ}\) | \text{°} ^{\circ} | 45\text{°} 45^{\circ} |
| \(\triangle ABC\equiv\triangle DEF\) | \equiv | \triangle ABC\equiv\triangle DEF |
| \(\triangle\text{ABC}\equiv\triangle\text{DEF}\) | \text{ } | \triangle\text{ABC}\equiv\triangle\text{DEF} |
| \(\triangle ABC\text{∽}\triangle DEF\) | \text{∽} | \triangle ABC\text{∽}\triangle DEF |
| \(\unicode{x2234}\) \(\unicode{x2235}\) | \unicode{番号} \unicode{番号} | \unicode{x2234} \unicode{x2235} |
| \(\therefore\) \(\because\) | \therefore \because | \therefore \because *ver3.5で確認。2.7表示ではせず。 |
| \(\subset \) | \subset | \subset |
| \(\supset \) | \supset | \supset |
| \(\in \) | \in | \in |
| \(\ni \) | \ni | \ni |
| \(\notin \) | \notin | \notin |
| \(\cap \) | \cap | \cap |
| \(\cup \) | \cup | \cup |
| \(\forall x \) | \foral | \forall x |
| \(\exists x \) | \exists | \exists x |
| \(\top \) | \top | \top |
| \(\bot \) | \bot | \bot |
| \(\land\) \(\lor\) \(\lnot\) \(\oplus\) \(\otimes\) \(\ominus\) | \land \lor \lnot \oplus \otimes \ominus | \land \lor \lnot \oplus \otimes \ominus |
| \(\varnothing\) \(\ltimes\) \(\rtimes\) | \varnothing \ltimes \rtimes | \varnothing \ltimes \rtimes *ver3.5で確認。2.7表示ではせず。 |
| \( \iff \) | \iff | \iff |
| \( \Rightarrow \) \( \Longrightarrow \) | \Rightarrow \Longrightarrow | \Rightarrow \Longrightarrow |
| \( \Leftarrow \) \( \Longleftarrow \) | \Leftarrow \Longleftarrow | \Leftarrow \Longleftarrow |
| \( \Leftrightarrow \) \( \Longleftrightarrow \) | \Leftrightarrow \Longleftrightarrow | \Leftrightarrow \Longleftrightarrow |
| \(\rightarrow \) \( \longrightarrow \) | \rightarrow \longrightarrow | \rightarrow \longrightarrow |
| \(\leftarrow \) \(\longleftarrow \) | \leftarrow \longleftarrow | \leftarrow \longleftarrow |
| \(\leftrightarrow \) \(\longleftrightarrow \) | \leftrightarrow \longleftrightarrow | \leftrightarrow \longleftrightarrow |
| \(\underleftarrow{AB\; example}\) | \underleftarrow{文字} | \underleftarrow{AB\; example} *半角スペースは無視される。\;等を使う |
| \(\mapsto\) | \mapsto | \mapsto |
| \(\hookleftarrow\) | \hookleftarrow | \hookleftarrow |
| \(\hookrightarrow\) | \hookrightarrow | \hookrightarrow |
| \(\searrow \) | \searrow | \searrow |
| \(\nearrow \) | \nearrow | \nearrow |
| \( \text{∅} \) \(\emptyset\) | \text{∅} \emptyset | \text{∅} \emptyset |
| \(5x+y=13\\14x+2y=8\) | \\ 改行 | 5x+y=13\\14x+2y=8 |
| \(\cases{3x + 2y = 13\\5x + 3y = 21}\) | \cases{数式1\\数式2} | \cases{3x + 2y = 13\\5x + 3y = 21} |
| \(\left\{\begin{array}{l}3x + 2y = 13\\5x + 3y = 21\end{array}\right.\) | \left\{¥begin{array}{l}数式1\\数式2\end{array}\right.\) | \left\{¥begin{array}{l}3x + 2y = 13\\5x + 3y = 21\end{array}\right. ★注意!:¥を半角\に置き換える事。 |
| \(f(x) =\begin{cases}\infty & (x = 0) \\ 0 & (x \neq 0) \end{cases} \) | ¥begin{cases}数式 & (条件) \\ 数式 & (条件) \end{cases} | f(x) =¥begin{cases}\infty & (x = 0) \\ 0 & (x \neq 0) \end{cases} ★注意!:¥を半角\に置き換える事。 |
| \(\sin \alpha\) | \sin | \sin \alpha |
| \(\cos \beta\) | \cos | \cos \beta |
| \(\tan \theta\) | \tan | \tan \theta |
| \(\exp(x)\) | \exp(数式) | \exp(x) |
| \(\log{_2} x\) | \log{底} | \log{_2} x |
| \(\log x\) | \log | \log x |
| \(\displaystyle \lim_{h \to 0} \frac{\sqrt{a+h}-\sqrt{a}}{h}\) | \to | \displaystyle \lim_{h \to 0} \frac{\sqrt{a+h}-\sqrt{a}}{h} |
| \(\displaystyle \lim_{h \to 0} \frac{\sqrt{\mathstrut a+h}-\sqrt{\mathstrut a}}{h}\) | \mathstrut *ルートの高さ合わせ | \displaystyle \lim_{h \to 0} \frac{\sqrt{\mathstrut a+h}-\sqrt{\mathstrut a}}{h} |
| \(f'(x)\) | f'(x) | |
| \(\displaystyle \frac{dy}{dx}\) | \frac{ 分子 }{ 分母 } | \displaystyle \frac{dy}{dx} |
| \(\displaystyle \frac{\mathrm{d} y}{\mathrm{d} x}\) | \frac{\mathrm{文字} 文字}{\mathrm{文字} 文字} | \displaystyle \frac{\mathrm{d} y}{\mathrm{d} x} |
| \(\displaystyle \frac{ \partial f }{ \partial x } \) | \partial | \displaystyle \frac{ \partial f }{ \partial x } |
| \(\displaystyle \lim_{ \Delta x \to 0 } \frac{ f(x + \Delta x) - f(x) }{ \Delta x }\) \(\displaystyle \lim_{ \Delta x \to -\infty } \frac{ f(x + \Delta x) - f(x) }{ \Delta x }\) | \lim_{ \Delta x \to 0 } \lim_{ \Delta x \to -\infty } | \displaystyle \lim_{ \Delta x \to 0 } \frac{ f(x + \Delta x) - f(x) }{ \Delta x } \displaystyle \lim_{ \Delta x \to -\infty } \frac{ f(x + \Delta x) - f(x) }{ \Delta x } |
| \(\displaystyle \sum_{k=1}^{n}k^2\) | \sum_{下}^{上} | \displaystyle \sum_{k=1}^{n}k^2 |
| \(\displaystyle \sum_{\substack{ 1\lt i\lt 3 \\ 1\le j\lt 5 }} a_{ij}\) | \displaystyle \sum_{\substack{ 上段 \\下段}} | \displaystyle \sum_{\substack{ 1\lt i\lt 3 \\ 1\le j\lt 5 }} a_{ij} *ver3.5で確認。2.7表示ではせず。 |
| \(\prod_{ i = 0 }^n x_i \) | \prod_{下}^{上} | \prod_{ i = 0 }^n x_i |
| \(\displaystyle \int_0^1 f(x) dx\) | \int_下^上 \int_{下}^{上} | \displaystyle \int_0^1 f(x) dx |
| \(\displaystyle \oint_0^1 f(x) dx\) | \oint_下^上 \oint_(下)^(上} | \displaystyle \oint_0^1 f(x) dx |
| \( {}_n \mathrm{C}_k \) | {}_下 \mathrm{文字} | {}_n \mathrm{C}_k |
| \(\langle a,b \rangle\) \(\left\langle{a}\middle|b\right\rangle\) \(\displaystyle \left\langle\frac{a}{2}\middle|b\right\rangle\) \(\displaystyle \left\langle {a},b\right\rangle\) | \langle {文字} \rangle \left\langle{文字}\middle|{文字}\right\rangle\) \displaystyle \left\langle\frac{文字}{文字}\middle|{文字}\right\rangle \displaystyle \left\langle {文字},{文字}\right\rangle\ | \langle a,b \rangle \left\langle{a}\middle|b\right\rangle \displaystyle \left\langle\frac{a}{2}\middle|b\right\rangle \displaystyle \left\langle {a},b\right\rangle |
| \(\displaystyle \braket{a|\frac{1}{2}}\) \(\bra{a}\) \(\displaystyle \ket{\frac{1}{2}}\) | \braket{文字} \bra{文字} \ket{文字} | \braket{a} \bra{a} \ket{\frac{1}{2}} *ver3.5で確認。2.7表示ではせず。 |
| \(\vec{a}\) \(\acute{a}\) \(\grave{a}\) \(\hat{a}\) \(\bar{a}\) \(\breve{a}\) \(\check{a}\) \(\tilde{a}\) \(\dot{a}\) \(\ddot{a}\) \(\mathrm{a}\) \(\ell\) \(\hbar\) | \vec{文字} \acute{文字} \grave{文字} \hat{文字} \bar{文字} \breve{文字} \check{文字} \tilde{文字} \dot{文字} \ddot{文字} \mathrm{文字} \ell \hbar | \vec{a} \acute{a} \grave{a} \hat{a} \bar{a} \breve{a} \check{a} \tilde{a} \dot{a} \ddot{a} \mathrm{a}--普通文字 \ell \hbar |
| \(\xcancel{1234}\) \(\bcancel{123}\) \(\cancel{12}\) \(\dddot{a}\) \(\ddddot{abc}\) | \xcancel{文字} \bcancel{文字} \cancel{文字} \dddot{文字} \ddddot{文字} | \xcancel{1234} \bcancel{123} \cancel{12} \dddot{a} \ddddot{abc} *ver3.5で確認。2.7表示ではせず。 |
| \( \overline{Z-a+3} \) | \overline{ 複数文字 } | \overline{Z-a+3} |
| \(\overrightarrow{ab}\) | \overrightarrow{文字} | \overrightarrow{ab} |
| \(\mathbf{a}\) | \mathbf{文字} | \mathbf{a} |
| \(\boldsymbol{a}\) | \boldsymbol{文字} | \boldsymbol{a} |
| \(x^\top\) | ^\top | x^\top |
| \({}^\exists\varepsilon\) | {}^\記号 | {}^\exists\varepsilon |
| \(A = \left( \begin{array}{ccc} a & b & c \\ d & e & f \\ g & h & i \end{array} \right)\) | \left( ¥begin{array}{ccc} 上式 & 上式 & 上式 \\ 中式 & 中式 & 中式 \\ 下式 & 下式 & 下式 \end{array} \right) *¥は半角\に置換。 | A = \left( ¥begin{array}{ccc} a & b & c \\ d & e & f \\ g & h & i \end{array} \right) ★注意!:¥を半角\に置き換える事。 begin{array}{cc}:中央揃え begin{array}{rr}:右揃え begin{array}{ll}:左揃え cc, rr, llは列数に合わす。 4列の場合は、 begin{array}{cccc}:中央揃え |
| \(A=\begin{pmatrix} 5 & 3 \\ 7 & 2 \end{pmatrix}\) | ¥begin{pmatrix} 上式 & 上式 \\下式 & 下式 \end{pmatrix} *¥は半角\に置換。 | A=¥begin{pmatrix} 5 & 3 \\ 7 & 2 \end{pmatrix} ★注意!:¥を半角\に置き換える事。 *{ccc}は使用できない。 |
| \(A=\begin{bmatrix} 5 & 3 \\ 7 & 2 \end{bmatrix}\) | ¥begin{bmatrix} 上式 & 上式 \\下式 & 下式 \end{bmatrix} *¥は半角\に置換。 | A=¥begin{bmatrix} 5 & 3 \\ 7 & 2 \end{bmatrix} ★注意!:¥を半角\に置き換える事。 |
| \(A=\begin{vmatrix} 5 & 3 \\ 7 & 2 \end{vmatrix}\) | ¥begin{vmatrix} 上式 & 上式 \\下式 & 下式 \end{vmatrix} *¥は半角\に置換。 | A=¥begin{vmatrix} 5 & 3 \\ 7 & 2 \end{vmatrix} ★注意!:¥を半角\に置き換える事。 |
| \(\mathbb{N}\) \(\mathbb{Z}\) \(\mathbb{R}\) \(\mathbb{C}\) \(\mathbb{ABCDEFG}\) | \(\mathbb{N}\):自然数全体 \(\mathbb{Z}\):整数全体 \(\mathbb{R}\):実数全体 \(\mathbb{C}\):複素数全体、実数全体 白抜き文字 | \mathbb{N} \mathbb{Z} \mathbb{R} \mathbb{C} \mathbb{ABCDEFG} |
| \(\mathcal{ABCDEF}\) \(\mathcal{L}\) \(\mathfrak{ABCDEF}\) \(\aleph\) \(\Re x, \Im x\) | \mathcal{文字} \mathcal{文字} \mathfrak{文字} \aleph \Re x, \Im x | \mathcal{ABCDEF} \mathcal{L} \mathfrak{ABCDEF} \aleph \Re x, \Im x |
| \(\triangle\) \(\diamond\) \(\ast\) \(\star\) \(\bullet\) \(\circ\) \(\unicode{x2642}\) \(\unicode{x2640}\) \(\unicode{x2713}\) \(\unicode{x2714}\) \(\unicode{x25AA}\) \(\unicode{x25AB}\) | \triangle \diamond \ast \star \bullet \circ \unicode{x2642} \unicode{x2640} \unicode{x2713} \unicode{x2714} \unicode{x25AA} \unicode{x25AB} | \triangle \diamond \ast \star \bullet \circ \unicode{x2642} \unicode{x2640} \unicode{x2713} \unicode{x2714} \unicode{x25AA} \unicode{x25AB} |
| \(\checkmark\) \(\boxplus\) \(\square\) | \checkmark \boxplus \square | \checkmark \boxplus \square *ver3.5で確認。2.7表示ではせず。 |
| \(\hat{x}_t = H_t x_{t-1} + u_t \tag{2.4a}\) | \式 \tag{文字} | \hat{x}_t = H_t x_{t-1} + u_t \tag{2.4a} * \tagを付けると自動的に式が中央揃え表示になる。 |
| \(\underset{\beta \in \mathbb{R}^p}{argmin}\) | \underset{下文字}{上文字} | \underset{\beta \in \mathbb{B}^p}{argmin} |
| \(\overbrace{ a_1 + \cdots + a_n }^{ n }\) | \overbrace{複数変数 }_{文字 } | \overbrace{ a_1 + \cdots + a_n }^{ n } |
| \(\underbrace{ a_1 + \cdots + a_n }_{ n }\) \(\underbrace{ a_1 + \cdots + a_n }_{ n }^{(note \;note)}\) | \underbrace{複数変数 }_{文字 } \underbrace{複数変数 }_{文字 }^{上文字} | (\underbrace{ a_1 + \cdots + a_n }_{ n } \underbrace{ a_1 + \cdots + a_n }_{ n }^{(note \;note)} |
ギリシャ文字表記一覧表
| 文字 | 記号名 | 記述方法 | 数学での意味 |
|---|---|---|---|
| \(\alpha \) | アルファ | \alpha | 第1種の過誤の確率、有意水準、回帰モデルの切片、クロンバックのアルファ。 とりあえず文字を使いたい一つ目の記号。 |
| \( \beta \) | ベータ | \beta | ベータ関数(大文字)、ベータ線、第2種の過誤の確率、偏回帰係数。 とりあえず文字を使いたい二つ目の記号。 |
| \( \gamma \) | ガンマ | \gamma | グッドマン=クラスカルのガンマ。 比熱比、オイラー定数。 とりあえず文字を使いたい三つ目の記号。 |
| \(\Gamma \) | ガンマ(大文字) | \Gamma | ガンマ関数 |
| \(\delta \) | デルタ | \delta | 変化量、デルタ関数、ラプラシアン、行列式 |
| \( \Delta \) | デルタ(大文字) | \Delta | |
| \(\nabla\) | ナブラ | \nabla | |
| \(\epsilon \) | イプシロン | \epsilon | 回帰モデルの誤差項 |
| \(\varepsilon \) | イプシロン | \varepsilon | |
| \(\zeta \) | ゼータ | \zeta | |
| \(\eta \) | エータ | \eta | 相関比(\(\eta^2\)) |
| \(\theta \) | シータ | \theta | 母数、定数、推定値 |
| \(\vartheta \) | シータ | \vartheta | |
| \( \Theta \) | シータ(大文字) | \Theta | |
| \(\iota \) | イオタ | \iota | |
| \( \kappa \) | カッパ | \kappa | コーエンのカッパ係数 |
| \(\lambda \) | ラムダ | \lambda | ウィルクスのラムダ(大文字)、グッドマン=クラスカルのラムダ、 ポアソン分布のパラメータ、固有値 |
| \(\Lambda \) | ラムダ(大文字) | \Lambda | |
| \( \mu \) | ミュー | \mu | 母平均 |
| \( \nu \) | ニュー | \nu | 自由度 |
| \(\xi \) | クシー | \xi | パラメータに使われる、大部分配関数 |
| \(\Xi \) | クシー(大文字) | \Xi | |
| \( o \) | オミクロン | o | |
| \(\pi \) | パイ | \pi | 円周率 |
| \( \Pi \) | パイ(大文字) | \Pi | 総乗 |
| \(\varpi\) | パイ(異体字) ポメガ | \varpi | 各周波数(流体力学) |
| \(\rho \) | ロー | \rho | 相関係数、密度 |
| \( \varrho \) | ロー | \varrho | |
| \(\sigma \) | シグマ | \sigma | 母分散(\(\sigma^2 \))、母標準偏差 |
| \( \varsigma \) | シグマ(異体字) | \varsigma | |
| \( \Sigma \) | シグマ(大文字) | \Sigma | 総和 |
| \( \tau \) | タウ | \tau | ケンドールのタウ、グッドマン=クラスカルのタウ |
| \( \upsilon \) | ウプシロン | \upsilon | |
| \( \Upsilon \) | ウプシロン (大文字の異体字) | \Upsilon | |
| \(\phi \) | ファイ | \phi | 自由度、オイラーのファイ関数、角度、特性関数(確率論)、ポテンシャル、波動関数 |
| \( \varphi \) | ファイ | \varphi | |
| \( \Phi \) | ファイ(大文字) | \Phi | |
| \( \chi \) | カイ | \chi | カイ二乗分布の検定統計量(\( \chi ^2\)) |
| \(\psi \) | プサイ | \psi | 波動関数 |
| \( \Psi \) | プサイ(大文字) | \Psi | 対比(多重比較) |
| \(\omega \) | オメガ | \omega | 角速度 |
| \( \Omega \) | オメガ(大文字) | \Omega | 抵抗 |
式を揃えて表示(応用1)
eqalign (簡単)
\(\displaystyle \eqalign{\int f(x) \,dx &= \int f(g(t)) \frac{dx}{dt} \,dt \\ &= \int f(g(t))g’(t) \,dt} \)
最初に¥eqalign{と最後に}につける。\displaystyleを付けないと積分記号等は1行表示になる。(¥は半角\に置き換えてください)=の前に&を付ける。 \\で改行する。
¥displaystyle \eqalign{\int f(x) \,dx &= \int f(g(t)) \frac{dx}{dt} \,dt \\ &= \int f(g(t))g’(t) \,dt}
begin{align}
\begin{align}\int f(x) \,dx &= \int f(g(t)) \frac{dx}{dt} \,dt \\ &= \int f(g(t))g’(t) \,dt \end{align}
¥begin{align}と\end{align}を最初と最後につける。(¥は半角\に置き換えてください)=の前に&を付ける。 \\で改行する。
¥begin{align}\int f(x) \,dx &= \int f(g(t)) \frac{dx}{dt} \,dt \\ &= \int f(g(t))g’(t) \,dt \end{align}
式に色付け (応用2)
Mathjaxで色付け
\begin{align}\int f(x) \,dx &\color{red}{= \int f(g(t)) \frac{dx}{dt} \,dt} \\ &\color{blue}{= \int f(g(t))g’(t) \,dt} \end{align}
\color{色}{数式} {}で数式を囲む。 但し、上記のアライメント用の&は\colorの外でないとアライメントが機能しない。
¥begin{align}\int f(x) \,dx &\color{red}{= \int f(g(t)) \frac{dx}{dt} \,dt} \\ &\color{gray}{= \int f(g(t))g’(t) \,dt} \end{align}
red, yellow, blue, green, white, gray, cyan, black
おしゃれな色付け
\(\color{red}{\xcancel{\color{black}{123}}} \color{red}{321}\)
\color{red}{\xcancel{\color{black}{123}}} \color{red}{321}
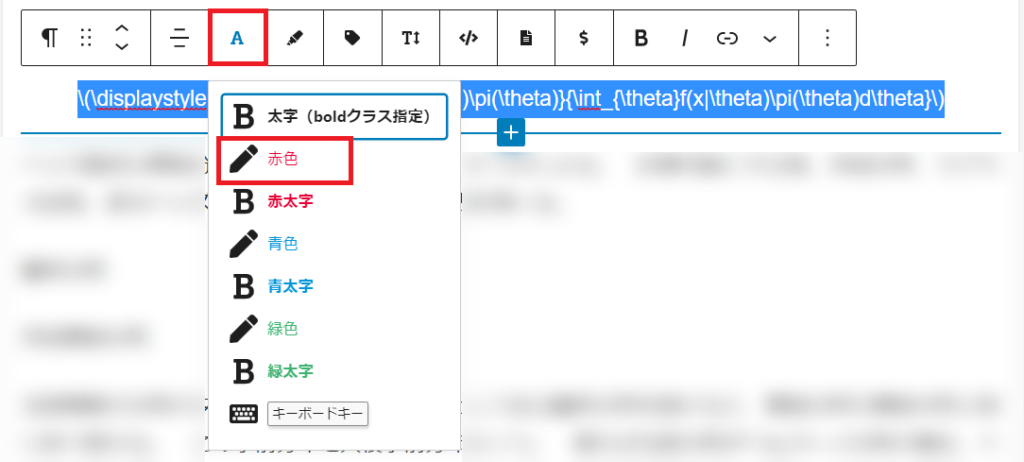
ワードプレスの書式で色付け(簡単)
数式を選択して『A』=>『赤字』(色)を選択すると、色付けできました。 しかし部分的な色付けは出来ないようです。(赤太字を選んでも色は付きましたが、太字にはなりませんでした。)
その他
表
注意)¥は半角\に置き換えてください。 また下のコードをコピペした時、改行記号の半角\が2個必要なところが、何故か1個になっててエラーになりました。 \hlineの前の\を\\に戻すと正常に表示されました。
¥begin{array}{c|ccccc} x & \cdots & -1 & \cdots & 1 & \cdots \\ \hline f’(x) & + & 0 & – & 0 & + \\ \hline f(x) & \nearrow & e & \searrow & -e & \nearrow \end{array}
\begin{array}{c|ccccc} x & \cdots & -1 & \cdots & 1 & \cdots \\ \hline f’(x) & + & 0 & – & 0 & + \\ \hline f(x) & \nearrow & e & \searrow & -e & \nearrow \end{array}
大きな行列
注意)¥は半角\に置き換えてください。また下のコードをコピペした時、改行記号の半角\が2個必要なところが、何故か1個になっててエラーになりました。 \hlineの前の\を\\に戻すと正常に表示されました。
{cccc}は列のアライメント用で列数分だけcが必要。
1列目以外は先頭にアライメント用に&が必要。
\vdotsーーー縦3ドット
\ddotsーーー横3ドット
\ldotsーーー右斜下3ドット
\begin{eqnarray}\left(\begin{array}{cccc}x_{ 11 } & x_{ 12 } & \ldots & x_{ 1n } \\x_{ 21 } & x_{ 22 } & \ldots & x_{ 2n } \\ \vdots & \vdots & \ddots & \vdots \\ x_{ m1 } & x_{ m2 } & \ldots & X_{ mn }\end{array}\right)\end{eqnarray}
\begin{eqnarray}\left(\begin{array}{cccc}x_{ 11 } & x_{ 12 } & \ldots & x_{ 1n } \\x_{ 21 } & x_{ 22 } & \ldots & x_{ 2n } \\ \vdots & \vdots & \ddots & \vdots \\ x_{ m1 } & x_{ m2 } & \ldots & X_{ mn }\end{array}\right)\end{eqnarray}
枠で囲む (2.7では表示しなかった)
\enclose
細かくしていできませんが、角が取れた長方形になります。数式の色もmathcolorの色と同じになります。なので、以下のサンプルでは、文字を黒に指定しています。
\(\displaystyle K=\frac{PH^T}{\enclose{roundedbox}[mathcolor=red]{\color{black}{R+HPH^T}}}\)
\displaystyle K=\frac{PH^T}{\enclose{roundedbox}[mathcolor=red]{\color{black}{R+HPH^T}}}
\bbox
細かく指定できますが長方形になります。
\(\bbox[yellow, 5px, border: 2px dotted red]{f(x)=\frac{1}{x^2} \cdot \frac{z}{y}} \)
\bbox[yellow, 5px, border: 2px dotted red]{f(x)=\frac{1}{x^2} \cdot \frac{z}{y}}
\boxed
一番簡単
\(\boxed{f(x)=x^2+y^2}\)
\boxed{f(x)=x^2+y^2}
5pxはpadding。2pxは枠の太さdotted,solid
エラー表示となった表記一覧 (バージョン違い)
バージョン3.5でも使えなかった。
- \rightarpoonup, \rightarpoondown, \leftarpoonup, \leftarpoondown, \leftrigtharpoons, \nothing, \box
- \usepackage{physics}
バージョン3.5では使えたが、2.7では使えなかった
*Mathjaxも色々バージョン、以下の表記は、私のMathjaxバージョン(2.7)環境では表示されませんでした。 thereforeやcheckmarkやleqq等は使いたいのですがね。
- \therefore, \because
- \dddot, \ddddot
- \fallingdotseq, \risingdotseq, \leqq, \geqq, \veebar, \varnothing, \triangleq
- \ltimes, \rtimes, \backsim
- \braket, \bra, \ket, \substack
- \require{enclose}
上記のエラーとなった表記も使うより前(上)に、\require{cancel}と書いておけば\cancelは使える。xcancel, bcancel, because, therefore, mathtip, texttipは認識されなかった。
マクロで表示
ページに以下のマクロを書き込む事で、<>等のブラケットの表示が可能となりましたが、マクロを書いた部分が空白の余白表示になりました。 マクロは<>等の記述部分より上に書き込まねば表示されませんでした。
\newcommand\bra[1]{\mathinner{\langle{#1}|}}
\newcommand\ket[1]{\mathinner{|{#1}\rangle}}
\newcommand\braket[1]{\mathinner{\langle{#1}\rangle}}
\newcommand\Bra[1]{\left\langle#1\right|}
\newcommand\Ket[1]{\left|#1\right\rangle}
\newcommand\Braket[1]{\left\langle #1 \right\rangle}
この下にマクロを書いたが、空白になっている。
\(\newcommand\bra[1]{\mathinner{\langle{#1}|}}\)
\(\newcommand\ket[1]{\mathinner{|{#1}\rangle}}\)
\(\newcommand\braket[1]{\mathinner{\langle{#1}\rangle}}\)
\(\newcommand\Bra[1]{\left\langle#1\right|}\)
\(\newcommand\Ket[1]{\left|#1\right\rangle}\)
\(\newcommand\Braket[1]{\left\langle #1 \right\rangle}\)
\(\braket{a|A|b}\)
\(\ket{a}\)
\(\braket{{\phi}|{a}}\)
\(\Bra{\displaystyle \frac{a}{3}}\)
\(\Braket{\displaystyle \frac{\psi}{4}\Bigg|{a}}\)
上記のブラケット<>表記は、以下の様に記述しています。
\braket{a|A|b}
\ket{a}
\braket{{\phi}|{a}}
\Bra{\displaystyle \frac{a}{3}}
\Braket{\displaystyle \frac{\psi}{4}\Bigg|{a}}
$$を上下に挟む方法もある。
\newcommandの代わりに\defも使用できる。
$$
\def\bra#1{\left\langle{#1}\right|}}
\def\ket#1{\left|{#1}\right\rangle}}
\def\braket#1#2{\left\langle{#1}\middle|#2\right\rangle}
$$



コメント