数学分布まとめ（一覧表、Pyro関数、用語など）

作成中。PCで横長で表示した方がいいです。

ベイジリアン推論をする際、事前分布や事後分布やどれを選択するのかとか、入力するパラメータの意味等分からないのでまとめ始めました。　2つ目の表はPyroの分布の関数で使う時の引数とその役割説明です。

分布一覧（式、意味）

分布名 Distribution name	式 Equation	概要 Remarks
連続型一様分布 continuous uniform （連続:continuous)	\(\displaystyle f(x\|a,b) =\frac{1}{b-a} \qquad \) \( \qquad (a\leq x\leq b) \\ =0 \qquad (x < a, x>b)\) \(\displaystyle E[X]= \frac{a+b}{2}\\ \displaystyle V[X]=\frac{(b-a)^2}{12}\)	完全にランダムな事象の場合。 Uniform(\(-\infty,\infty\))はimproperな事前分布。グループ数が小さい場合、一様分布は事後分布への影響大。　（ー＞HalfCauchy分布を使う。） Uniform(0､b)として大きなbを使う。弱情報事前分布の場合、考えられる分散（弱情報）をbに入れておくる。
ベルヌーイ分布 Bernoulli （離散:dicrete)	\(\displaystyle f(x;p)=p^x(1-p)^{}1-x \\ \qquad(x \in(1,0))\) \(\mu=p, \sigma^2=p(1-p)\)	二項分布で回数が1回か０回しかない場合の分布。　試行を２回以上の場合は二項分布。共役事前分布はベータ分布。
二項分布 Binomial （離散:dicrete）	\(f(k\|p,N)={}_N \mathrm{C}_kP^N(1-p)^{N-k}\) \(E[X]=Np \\ V[X]=Np(1-p)\) \(\phi(t)=(1-p+pe~{it})^N\)	成功か失敗しかない試行をN回繰返し、k回成功する確率。視聴率の推定。（二項分布->正規近似）共役事前分布はベータ分布。
負の二項分布 negative binomial （離散：discrete)	\(\displaystyle f(k\|r,p) =\begin{pmatrix} k+r-1 \\ k \end{pmatrix}(1-p)^rp^k \) \(\displaystyle E[X]=\frac{pr}{1-p}\\ \displaystyle V[X]=\frac{pr}{(1-p)^2}\)	平均発生数が一定と仮定できない(ポアソン分布が適しない)計数推定に利用できる。 r 回の失敗までに k 回の成功が起こる確率。無限分解分布
多項分布 Multinomial （離散:dicrete）	\(\displaystyle f(m\|\mu,N)\) \(\displaystyle=\frac{N!}{m_1!, \cdots , m_K!}p_1^{m_1}\) \( \qquad \displaystyle \cdots p_K^{m_K} \frac{N!}{m_1!, \cdots , m_K!}\prod_{i \to 1}^K \mu_i^{m_i} \)	複数(N回)試行する二項（成功か失敗）の項目を1~6の様に３以上の多項（K>2）の分布。 \(m_i\)は\(i\)の項目が出た回数。　\(p_i\)は\(i\)が出る確率。　出た順番は関係ない。 \(\sum_{k=1}^k \mu_k=\sum_{k=1}^k p_k=1\) N=1の多項分布がカテゴリカル分布。共役事前分布はディリクレ分布。
カテゴリカル分布 Categorical （離散:dicrete）	\(\displaystyle f(m\|\mu,K)\\=p_1^{m_1} \cdots p_K^{m_K} \\ \displaystyle =\prod_{i \to 1}^K \mu_i^{m_i} \)	多項分布で試行回数がN=1の場合がカテゴリカル分布。またカテゴリカル分布のK=2とするとベルヌーイ分布。 \(\sum_{i=1}^K \mu_i=1\) 共役事前分布はディリクレ分布。
ディリクレ分布 Dirichlet (=多変量ベータ分布）（連続:continuous)	\(\displaystyle f(\mu_i\|\alpha_i) \\ \displaystyle =\frac{1}{B(\alpha)}\prod_{i=1}^{N} \mu_i^{\alpha_i-1} \) \(\displaystyle B(\alpha)=\frac{\prod_{i=1}^N\Gamma(\alpha_i)}{\Gamma(\sum_{i=1}^{N}\alpha_i)}=C\) (定数）	ベータ分布の多変量な場合。（多変量ベータ分布とも呼ばれる） N個の事象がそれぞれ\(\alpha_i-1\)回発生した時の確率\(\mu_i\)を求める。多項分布（二項分布@N=2）の共役事前分布。混合モデルに使われる。条件\(\sum_{i \to 1}^N \mu_i^{\alpha_{i-1}}=1, \alpha_i \in \mathbb{R}>0\)
ベータ分布(１種） Beta distribution of the first kind （連続:continuous)	\(\displaystyle f(p\|\alpha,\beta) \\=\displaystyle \frac{p^{\alpha-1}(1-p)^{\beta-1}}{B(\alpha, \beta)} \\ \quad (0 \leq p\leq1)\) ベータ関数\(\displaystyle B(\alpha,\beta) =\frac{\Gamma (\alpha) \Gamma (\beta)}{\Gamma(\alpha+\beta)}\) \(\displaystyle E[X]=\frac{\alpha}{\alpha+\beta} \\ \displaystyle V[X]=\frac{\alpha\beta}{(\alpha+\beta)^2(\alpha+\beta+1)}\)	ディリクレ分布のN=2。ベイズ統計でよく使われる。\(\alpha\)は事象発生回数、\(\beta\)は発生しなかった回数。両方とも、形状(shape)母数。固定された範囲を上回る可能性を表す場合。[efn_note]これが\(\displaystyle \int_{-\infty}^{\infty} \frac{(x-\mu)^2}{\sigma^2}dx\)[/efn_note] 二項分布のprobsに与える共役事前分布。 Beta(0.5,0.5)はJeffreys事前分布。（無情報事前分布？） Beta(0,0)はimproperな事前分布。
正規分布 Normal （=ガウス分布：Gaussian）（連続: continuous)	\(\displaystyle f(x\|\mu,\sigma^2)\\=\displaystyle \frac{1}{\sqrt{2 \pi \sigma^2}}\exp\left(-\frac{(x-\mu)^2}{2\sigma^2}\right)\)	ランダムノイズ、中心極限定理カーネル密度推定 Normal(\(\mu,\sigma\)) 無限分解可能分布
多変量正規分布 Multivariate Normal （連続: continuous)	\(\displaystyle X ~\mathcal{N}_k(\mu_i, \Sigma_{ii})\) \(\displaystyle \mu=E[X]=(E[X_1],\cdots,E[X_k]\) \(\displaystyle \sum_{i,j}:=Cov[X_i,X_j]=E[(X_i-\mu_i)(X_j-\mu_j)]\)	混合ガウシアンでよく使う。分散共分散逆行列は精度行列(precision matrix)、\(Q=\Sigma^{-1}\)
対数正規分布 Log-normal （連続: continuous)	\(\displaystyle f(x\|\mu,\sigma^2)\\=\displaystyle \frac{1}{\sqrt{2 \pi \sigma^2}}\exp\left(-\frac{(\log x-\mu)^2}{2\sigma^2}\right)\) \(\displaystyle E[X]=\exp(\mu+\frac{\sigma^2}{2}) \\ V[X]=\exp(2\mu+\sigma^2)(\exp(\sigma^2)-1)\)	各人が保有する資産の分布に近い。株価 LogNormal(\(\mu,\sigma\))
t分布 Student's t （連続: continuous)	\(\displaystyle f(x\|n)=\frac{\displaystyle \Gamma(\frac{n+1}{2})}{\displaystyle \sqrt{n \pi} \, \Gamma(\frac{n}{2})}(1+ \frac{x^2}{n})^{-(\frac{n+1}{2})}\)	正規分布の試行数n（自由度）が少ない場合。正規分布の山が低く、すそ野が広がったグラフ。n\(\rightarrow \infty\)で正規分布に一致する。 t分布表。　平均は0。　分散当たりの%点は自由度により異なる。無限分解可能分布
多変量t分布 Multivariate student's t （連続: continuous)	\(f(x_i\|p,n,\mu_i,\Sigma_{ii}) \) \( =\displaystyle \frac{\displaystyle \Gamma(\frac{n+p}{2})}{(\sqrt{n \pi})^p\Gamma(\frac{n}{2})\|\Sigma\|^{\frac{1}{2}}}\) \( \displaystyle \qquad \times \left[1+\frac{1}{n}(x-\mu)^{\top} \Sigma^{-1}(x-\mu) \right]^{\displaystyle -\frac{(n+p)}{2}}\)	ランダムp次元ベクトルのt分布。 n:自由度　（n=1 \(\rightarrow \)多変量コーシー分布） \(x\): (p x 1)ベクトル \(\mu\):平均　(p x 1)ベクトル \(\Sigma\):\(\sigma\)のp x p行列としての記号。 \((x-\mu)^{\top\}): 縦ベクトルへの転置。
コーシー分布 Cauchy (＝ローレンツ分布） (＝ブライト・ワグナー分布（物理））（連続：continuous)	\(\displaystyle f(x\|\mu,\gamma)=\frac{1}{\pi \gamma \left\{1+\left(\frac{x-\mu}{\gamma}\right)^2 \right\}}\) \(\mu=0, \gamma=1\)の時、標準コーシー分布。期待値、分散が存在しない。	自由度1のt分布が標準コーシー分布。　期待値が存在しない。（大数の法則が成立しない）　裾が厚い分布の代表。(外れ値を取る確率が低い。）証券価格の大暴落などの滅多に起こらない事象をモデル化する場合など）正の範囲だけー＞半コーシー分布。グループ数が少ない時、階層分散パラメータの条件付共役事前分布。 \(\sigma_{\alpha}=0\)で最大値となり、なだらかに減少。 \(x\)が小さいとピークも低くすそ野が広がる。強制共鳴や分光学の共鳴広がり等スペクトル線形状。無限分解可能分布、安定分布 \(\mu\) location parameter 最頻値 \(\gamma\) scale parameter 半値半幅
ポアソン分布 Poisson （離散：discrete)	\(\displaystyle f(k\|\lambda)=e^{-\lambda} \frac{\lambda^k}{k!}\) \(E[X]= V[X]=\lambda\)	レアでランダムな事象が単位時間に\(\lambda\)数発生する場合の確率分布。　\(k\)：発生数交通事故の回数。　不良品の割合。病気に疾患する確率。二項分布と比べ、n->大、p->小さい、np=一定\((\lambda)\) 二項分布の近似で機械学習での計算が楽になる。無限分解可能分布
指数分布 exponential （連続: continuous)	\(\displaystyle f(t\|\mu)=\frac{1}{\mu}e^{-\frac{t}{\mu}}\\ =\lambda e^{-\lambda x}\\ \quad (t \leq 0)\) \(\displaystyle E[X]=\mu = \frac{1}{\lambda} \\ \displaystyle V[X]=\mu^2=\frac{1}{\lambda^2}\)	ランダムな事象の発生の平均時間間隔\(\mu\)の時、次に起こるまでの期間\(t\)の確率密度分布。機械故障間隔（MTBF)。　客到着間隔。実際確率を出すには、確率密度を経過時間（区間）で積分すると確率になる。 \(\displaystyle \lambda=\frac{1}{\mu}\)：単位時間内での発生回数。幾何分布の連続型。似ているが、ポアソン分布は離散型で、単位時間に\(\lambda\)回起こる現象がX回起こる確率分布で、時間経過を出すものでない。　指数分布＝＞期間　ポアソン分布＝＞回数
ワイブル分布 Weibull （＝最弱Ringモデル）（連続：continuous)	\(\displaystyle f(t\|\eta,m)\\ \displaystyle =\frac{m}{\eta}\left( \frac{t}{\eta}\right)^{m-1}\exp\left\{ -\left( \frac{t}{\eta}\right)^m\right\}\) \(\qquad (0 \text{<}x )\)	物体の強度を統計的に記述する為の分布。バスタブ曲線の様に、時間に対する劣化現象や寿命の場合。 \(\eta\): 尺度(scale)：発生平均時間の様なもの。--分布のピーク。 m:ワイブル係数（形状母数:shape)--分布のバラツキ。 m=1：指数分布ｍ=2：レイリー分布 m\(\rightarrow　\infty\)：正規分布 m<1:初期故障 m=1：偶発故障故障率のヒストグラムを作り、ワイブル確率子にプロットしmを読み取る。 m>1:摩耗・劣化故障
レイリー分布 Reyleigh （連続：continuous)	\(\displaystyle f(x\|\sigma^2)=\frac{x}{\sigma^2}e^{-\frac{x^2}{2\sigma^2}}\) \(\displaystyle E(x)=\sigma\sqrt{\frac{\pi}{2}} \\ \displaystyle V[X]=\left(2-\frac{\pi}{2}\right)\sigma^2\)	風力発電量予測、マイクロ波無線通信、移動無線通信の伝搬解析、超音波診断自由度２のワイブル乗分布
幾何分布 Geometric （離散：discrete)	\(\displaystyle f(k\|p)=p(1-p)^{k}\) \(\displaystyle E[X]=\frac{1}{p} \\ \displaystyle V[X]=\frac{1-p}{p^2}\)	既知な成功確率で、試行k+1回数内で成功する確率を求める場合。 p：成功率『離散的な待ち時間分布』無限分解分布
超幾何分布 Hyper-Geometric	\(\displaystyle P(X=x)=\frac{{}_M \mathrm{C}_{x} \cdot {}_{N-M} \mathrm{C}_{n-x}}{{}_N \mathrm{C}_n}\) \(\displaystyle E[X]=\frac{KM}{N} \\ V[X]=\frac{K(N-K) \frac{M}{N}(1-\frac{M}{N})}{N-1}\)	当たりM個、外れN-M個のボール。　Kを取り出した時、当たりX個となる確率。既知の不良率で抜き取った標本の不適合個数の分散。薬（あり・なし）で発症を抑えたかどうか（発症・なし）を見る臨床実験。
ガンマ分布 Gamma （連続：continuous）	\(\displaystyle f(x\|n,\mu) =\frac{1}{ \mu^n　\Gamma(n)} x^{n-1} e^{-\frac{x}{\mu}}\\ \quad (0 \leq x)\) \(\displaystyle E[X]=n\mu\)：n回発生する平均時間 \( V[X]=n\mu^2\)：n回発生する時間分散	期間\(\mu\)内に１回起こるランダムな事象がｎ回起こるまでの時間の分布。指数分布に回数(n)を使えるよう一般化したものなので、指数分布と考え方は同じ。 \(x\)は時間。　\(f(x)\)はある時間の時に起こる確率 10年に1回起こる事象が２回起こるまでの年数。　電子部品の寿命分布。　通信トラフィック待ち時間。　所得分布。　ウィルスの潜伏期間。『連続的な待ち時間分布』無限分解可能分布 n=1の時が指数分布。　nを極大化すると正規分布。 n: 発生回数 \(=\alpha\) shape parameter \(\mu\):平均発生時間 \(=\beta\) 　scale parameter \(\lambda=\frac{1}{\mu}\): 単位時間発生回数 rate parameter
\(\chi^2\)分布 Chi-squared （連続：continuous）	\(\displaystyle Z \sim\chi_n^2 =f(x\|n)=\displaystyle \frac{1}{2^{\frac{n}{2}} \Gamma (\frac{n}{2} ) }x^{\frac{n}{2}-1}e^{-\frac{x}{2}} \\ \quad (0 < x)\)	独立に標準正規分布に従う k 個の確率変数 \(X_1,\cdots, X_n\) をとる時、\(Z=\sum_{i \to 1}^nX_i^2\)の事を自由度nのカイ二乗分布。ガンマ分布の\(n \to \frac{n}{2},\mu \to 2\)の場合がカイ二乗分布。カイ二乗検定やフリードマン検定等、推計統計学で多用される。　自由度\(n\)が大きくなると正規分布に近づく。カイ二乗分布表。カイ二乗分布の多次元はウィシャート分布。
逆ガンマ分布 Inverse gamma （連続：continuous)	\(\displaystyle f(x\|n,\mu)=\frac{\mu^n}{ \Gamma(n)} x^{-n-1} e^{-\frac{\mu}{x}}\\ \quad (0 \leq x)\) \(\displaystyle \Gamma(\alpha)=\int_0^{\infty}x^{-\alpha-1}e^{-\frac{\beta}{x}}\) \(\displaystyle E[X]=n\mu \\ V[X]=n\mu^2\)	正規分布の分散が不明の時の共役事前分布。 InvGamma(\(x_i,y_i\)) n: 発生回数 \(=\alpha\) 形状(shape) パラメータ \(\mu\):平均発生時間 \(=\beta\)　尺度(scale)パラメータ \(x\):単位時間当たりの発生回数 \(ｇ(x\|n,\mu)\)は、平均発生時間\(\mu\)の事象が、n回発生する確率密度分布で、単位時間当たりに\(x\)回発生する確率を表す関数。 (＊Andrew Gelmanによると階層分散パラメータの事前分布として使うべきでない？） InverseGamma(0,0)はimproperな事前分布。逆ガンマ分布の多次元が逆ウィシャート分布。
F分布 F distribution (=Fisher-Snedecor) （連続：continuous)	\(\displaystyle F(x\|\phi_1,\phi_2)=\frac{\displaystyle \frac{\phi_1}{\phi_2}^{\frac{\phi_1}{2}}}{\displaystyle B(\frac{\phi_1}{2},\frac{\phi_2}{2})} \frac{\displaystyle x^{\frac{\phi_1}{2}-1}}{\displaystyle (1+ \frac{\phi_1}{\phi_2}x)^{\frac{\phi_1+\phi_2}{2}}}\) \(\displaystyle F=\frac{\displaystyle \frac{\chi_1^2}{\phi_1}}{\displaystyle \frac{\chi_2^2}{\phi_2}}\)	\(F\)分布は自由度\(\phi_1. \phi_2\)であるカイ二乗分布\(\chi_1^2, \chi_2^2\)が独立の時の比。仮説検定の時よく使う。 \(\bullet\: F(1,\phi_2)=\{t(\phi_2)\}^2\) \(\bullet\: F(1,\infty)=\{t(\infty)\}^2=Z^2,Z\sim N(0,1)\) \(\bullet\: F(\phi_1,\infty)\rightarrow \chi^2(\phi_1)\) \(\bullet\: F(\infty,\infty)\rightarrow\chi^2(\infty)\sim\)　正規分布
フォンミーゼスフィッシャー分布 Von Mises Fisher (=circular normal) （連続：continuous)	\(\displaystyle f(x\|\mu,\kappa)\\ \displaystyle=\frac{e^{\kappa \cos(x-\mu)}}{2\pi I_0(\kappa)}\\=Ce^{\kappa \mu^{\top} x }\)	方向データに対する球面上における確率分布。 \(\|x\|=1\): 単位球面上、長さ１のベクトル。\(-\pi \leq x \leq \pi\) 平均方向(位置(location)パラメータ)：\(-\pi \leq \mu \leq \pi\) 集中度(形状(shape)パラメータ）：\(\kappa>0\) 大きくなるとピークが鋭くなる。　小さくなると裾が厚くなる。　0に近づくと一様に近づく。 \(C\)は定数。
ラプラス分布 Laplace （＝二重指数分布、両側指数分布）（連続：continuous)	\(\displaystyle f(x\|\mu,b)=\frac{1}{2b}\exp(-\frac{\|x-\mu\|}{b})\) \(\displaystyle E[X]=\mu \\ V[X]=2b^2\)	正規分布の中心を高くして、すそ野を広げた感じ。左右対称。音源・機密保護などに使われる。 bが小さい程ピークが高くなり、鋭くなる。bがほぼ0で、ピーク以外の確率密度は0になる。 \(\mu\)はピーク位置。位置(location)パラメータ
ガンベル分布 Gumbel (=二重指数分布) (=Extreme value Type I) （連続：continuous)	\(\displaystyle f(x\|\mu,\eta)\) \( \displaystyle=\frac{1}{\eta}\exp\left\{-\left(\frac{x-\mu}{\eta} \right)\right\}\exp\left[-\exp\left\{-\left(\frac{x-\mu}{\eta}\right)\right\}\right]\)	極値分布のタイプI。極値統計滅多に起こらない事象（洪水、台風、干ばつ等）右裾が厚くなる分布。 \(\mu\)位置(location)パラメータ \(\eta\) 尺度(scale)パラメータ
ロジスティック分布 Logistic （連続：continuous)	\(\displaystyle f(x\|\mu,\sigma) =\frac{\exp(-\frac{x-\mu}{\sigma})}{\sigma \left[1+\exp(-\frac{x-\mu}{\sigma})\right]^2}\)	正規分布と酷似していて左右対称。　ロジスティック分布の方が裾が長い。 \(\mu\) 位置 (location)パラメータ \(\sigma\) 尺度(scale)パラメータ
パレート分布 Pareto （連続：continuous)	\(\displaystyle f(x\|\alpha, \beta)=\frac{\alpha/\beta}{(x/\beta)^{\alpha+1}}\) \(\displaystyle E[X]=\frac{\alpha \beta}{\alpha-1}\quad(\alpha>1) \) \( \displaystyle V[X]=\frac{\alpha\beta^2}{(\alpha-1)^2(\alpha-2)} \quad (\alpha>2)\)	所得の分布をモデリングする分布。　離散型はゼータ分布。 \(\alpha\)形状(shape)パラメータ \(\beta\):尺度(scale)パラメータ
クマラスワミ分布 Kumaraswamy （連続：continuous)	\(f(x\|\alpha,\beta)=\alpha\beta x^{\alpha-1}(1-x^\alpha)^{\beta-1}\) \(0\leq x \leq 1\) \(\alpha>0, \beta>0\)	ベータ分布に類似だがもっと簡単。 \(\alpha,\beta\):形状(shape)パラメータ \(\alpha=1\)か\(\beta=1\)の時、ベータ分布と同じ。 Kuma(\(\alpha\),1)=Beta(\(\alpha\),1)
安定分布 Stable （＝安定パレート、レヴィ\(\alpha \)分布）	確率密度は特性関数を用いてしか表せれない。 \(\displaystyle f(x)=\frac{1}{2 \pi} \int_{-\infty}^{\infty} \varphi(t)e^{-ixt}dt\) 条件 \(S_n=\frac{1}{\alpha_n}\sum_{i=1}^n X_i-\beta_n \)	正規分布やコーシー分布を含む広い概念。　しかし、Pyroでは正規分布より裾野が重い分布を指しており、外れ値が多く、正規分布では精度がでにくい場合に正規分布に変わってStable分布を使う。パラメータは４つ（母数） \(\alpha\): 　裾野の重さを表す。　小さい程、すそ野が重い。 \(\beta\): 　歪を表す。　０の時、左右対称。 \(\alpha\):　規模を表す。 \(\alpha\):　平行移動。全ての\(\beta_n=0\)の時、厳密に安定（strictly stable)。
無限分解分布 Infinite divisibility(probability)	確率変数\(x_{n1},x_{n2}, \cdots , x_{nn}\)が\(F\)の分布の時、 \(Sn(=x_{n1}+x_{n2}+ \cdots + x_{nn})\)が同じ\(F\)分布となる時、\(F\)分布は無限分解分布。	任意の数の独立した同一分布の（i.i.d.）確率変数の合計の確率分布の種類の総称。　連続型では、正規分布、コーシー分布、t分布、ガンマ分布。離散型では、ポアソン分布、負の二項分布、幾何分布等。一様分布や二項分布は無限分解分布でない。それぞれの無限分解可能分布はレヴィ過程に対応している。

分布一覧（Pyro 関数・引数・sample出力メモ）

分布名 Distribution name	Torch.distributions関数名 \(\bullet\) 引数	補足
連続型一様分布 continuous uniform （連続:continuous)	Uniform(low=torch.tensor([0.0]), high=torch.tensor([5.0])) \(\bullet\) low(=a) – lower range:tensor/float \(\bullet\) high(=b)– upper range:tensor/float	sampleでは区間内の数値xを均等に返す。 log_prob(low\(\leq x\leq\)high)
ベルヌーイ分布 Bernoulli （離散:dicrete)	Bernoulli(probs=torch.tensor([0.3])) \(\bullet\) probs=None >0 :Tensor/Number \(\bullet\) logits=None: Tensor/Number *ContinuousBernoulli()	sampleは1か0を返す。 probsかlogitsのどちらかを使用。 probは１が出る確率。 logitは対数表記。 *ContinuousBernoulliのsampleはfloatで返す。
二項分布 Binomial （離散:dicrete）	Binomial(total_count=100, probs=torch.tensor([0.1 , 0.2, 0.8, 0.99])) \(\bullet\) total_count=1 >0 :Tensor/int \(\bullet\) probs=None >0 :Tensor \(\bullet\) logits=None: Tensor	sampleはN回試行した時の、各確率の成功回数が正の整数で出力される。 Multinomialと違い、total_countは各事象確率だけで使われる。　4事象で100の場合は、各事象確率*100（正規分布）となるので、トータル100とはならない。 log_prob(0\(\leq\)x\(\leq \infty\)) グラフ表示はプロットは整数のみ。　np.linspace等で小数になる場合はエラー。
負の二項分布 negative binomial （離散：discrete)	NegativeBinomial(total_count=10, probs=torch.tensor([0.5])) \(\bullet\) total_count=1 >0 :Tensor/float \(\bullet\) probs=None >0 :Tensor \(\bullet\) logits=None: Tensor	sampleはprobs(失敗確率=p）の失敗数(=total_count=r)までに成功する回数(=k)を正の整数で返す。 total_count(=r)：失敗数 probs(=p):失敗確率 (logits:失敗確率のLog） log_prob(0\(\leq\)k\(\leq \infty\) 整数のみ。　小数不可。
多項分布 Multinomial （離散:dicrete）	Multinomial(total_count=100, probs=torch.tensor([ 1., 1., 1., 1.])) \(\bullet\) total_count=1:tensor/int \(\bullet\) probs=None/tensor \(\bullet\) logits=None/tensor	sampleはBinomialと違い、total_countは全事象確率に分配される。　4事象で100の場合は、４つの0以上の正数でトータルで100となる。 total_count: tensorの場合は、各要素の数値をprobsの確率数で分配される。
カテゴリカル分布 Categorical （離散:dicrete）	Categorical(probs=torch.tensor([ 0.25, 0.25, 0.25, 0.25 ])) \(\bullet\) probs=None >0 :tensor \(\bullet\) logits=None:tensor	sampleはprobsで指定した確率に応じて番号(K-1:int)で出力。 probs: K個の各事象確率。全て足すと１。 logits: K個の各事象のlog確率（非正規化） N次元の時、最初のN-1次元はバッチとして扱われる。 probsかlogitsのどちらか使用。 4事象の無情報の場合([ 0.25, 0.25, 0.25, 0.25 ])) Normal、MultivariateNormalの\(\mu\)や\(sigma\)の選択として使われる。
ディリクレ分布 Dirichlet (=多変量ベータ分布）（連続:continuous)	Dirichlet(concentration =torch.tensor([0.5, 0.5])) \(\bullet\) concentration >0 :Tensor	sampleは、concentrationで指定した確率の要素数分の発生回数が出力する。 Categoricalの事象の確率pとして渡す。 concentrationはよく\(\alpha\)とされる。多変量なのでベクトル値。入力(\alpha=\alpha_1,\alpha_2, \cdots, \alpha_N\)は各事象の発生回数。　出力は各事象の発生確率。無情報は([0.5,0.5])が良く使われる。（＝ベータと同じ）
ベータ分布(１種） Beta distribution of the first kind （連続:continuous)	Beta(concentration1=torch.tensor([1.0]), concentration0 =torch.tensor([1.0])) \(\bullet\) concentration1 :Tensor/float \(\bullet\) concentration0 :Tensor/float	sampleは事象が発生する確率pを返す。共役事前分布としてBinomialのprobsに与える。無情報は([1.0,1.0])が良く使われる。 concentration1とconcentration0 はそれぞれよよく(\alpha, \beta\)で使われる。各事象の発生回数。　出力は各事象の発生確率。 log_prob(0\(\leq\)p\(\leq\)1)
正規分布 Normal （=ガウス分布：Gaussian）（連続: continuous)	Normal(loc=torch.tensor([0.0]),scale= torch.tensor([1.0])) \(\bullet\) loc(\(=\mu\):tensor/float \(\bullet\) scale(\(=\sigma\):tensor/float	sampleは\(\sigma(=x)\)の値を返す。 loc(=\(\mu\))：平均 scale(=\(\sigma\))：標準偏差無情報事前分布として標準正規分布のloc=([0.0]), scale=([1.0]) で使われる事が多い。 Normalの\(\mu(=loc)\)への渡しはNormalのsample出力から渡す。 Normalの\(\sigma(=scale)\)への渡しはInverseGammaのsample出力から渡す。 \(-\infty \)
多変量正規分布 Multivariate Normal （連続: continuous)	MultivariateNormal(loc=torch.zeros(2), covariance_matrix=torch.eye(2)) \(\bullet\) loc(\(=\mu\):tensor \(\bullet\) convariance_matrix=None:tensor \(\bullet\) precision_matrix=None:tensor \(\bullet\) scale_tril=None:tensor	sampleは各ベクトルの\(\sigma_i\)を返す。一括で複数の\(\sigma\)パラメータを生成できる。 \(\mu (loc)\)は(n x 1)次ベクトル。 \(\sum\)は(n x n)対角行列。torch.eye(n)等を使用。出力はn個。 locとcovariance_matrixで使われることが多い。下三角行列のscale_trilを使うのが最も有効。　loc以外の他の行列引数を使用した場合は、コレスキー分解で下三角行列を生成。 \(-\infty \)
対数正規分布 Log-normal （連続: continuous)	LogNormal(loc=torch.tensor([0.0]),scale= torch.tensor([1.0])) \(\bullet\) loc(\(=\mu\):tensor/float \(\bullet\) scale(\(=\sigma\):tensor/float	sampleは\(\sigma\)を返す。 0
t分布 Student's t （連続: continuous)	StudentT(df=torch.tensor([2.0])) \(\bullet\) df: tensor/float--自由度 \(\bullet\) loc=0.0: tensor/float--平均 \(\bullet\) scale=1.0:tensor/float--標準偏差	sampleは\(\sigma(=x)\)の値を返す。最低自由度(df)だけ入力必要。 -10\(\leq\)log_prob\(\leq\)10 で\(\pm10\sigma\)なので殆どカバーできる。 dfが2等小さい時は、\(\pm4\sigma\)ではカバーできない。
多変量t分布 Multivariate student's t （連続: continuous)	Multivarariate_studentt　（多変量） \(\bullet\) df--自由度 \(\bullet\) loc--平均 \(\bullet\) scale_tril--分散、下限三角行列。	sampleは(p x 1)次元のベクトルで\(\sigma_i(=x_i)\)の値を返す。 locのベクトルを見てp次元数を判断。
コーシー分布 Cauchy (＝ローレンツ分布） (＝ブライト・ワグナー分布（物理））（連続：continuous)	Cauchy(loc=torch.tensor([0.0]), scale=torch.tensor([1.0])) \(\bullet\) loc(=\(\alpha\)):tensor/float \(\bullet\) scale(=\(x\)):tensor/float *HalfCauchy(scale)---loc(=\(\alpha\))は内部で0で、設定できない。	sampleはxの値を返す。 loc(=\(\alpha\)): 分布のモードか中心値（ピーク） scale(=\(x\)): 半値半幅無情報事前分布として、loc=([0.0]), scale=([1.0])として与える。 Cauchyの場合：log_prob(\(-\infty \leq\)p\(\leq\infty\)) HalfCauchyの場合：log_prob(\(0
ポアソン分布 Poisson （離散：discrete)	Poisson(rate=torch.tensor([4])) \(\bullet\) rate(=\(\lambda \)>0:tensor	sampleは単位時間当たりの発生する個数(k)（正の整数） rate(=\(\lambda \):単位時間に発生する平均回数。　これが大きいほど、sample出力も大きくなる。 0\(\leq\)log_prob\(\leq \infty\) 整数のみ。　小数不可。
指数分布 exponential （連続: continuous)	Exponential(rate=torch.tensor([1.0])) \(\bullet\) rate (= 1 / scale):tensor/float	sampleは1/rateでの事象発生時間tを返す。 rateが大きいほど、発生確率は小さくなる。 0
ワイブル分布 Weibull （＝最弱Ringモデル）（連続：continuous)	Weibull(scale=torch.tensor([1.0]), concentration=torch.tensor([1.0])) \(\bullet\) scale (=\(\lambda\) :Tensor/float \(\bullet\) concentration (=k/shape):Tensor\float	sampleはt(tensor float)時間を返す。無情報として([1.0]),([1.0])が良く使われる。 scale:\(eta\)：大\(\rightarrow\)分布のピークが高くなる。 concentration:ワイブル係数（分布のバラツキ度合い。　大\(\rightarrow\)裾が厚くなる。）
レイリー分布 Reyleigh （連続：continuous)	なし Weibull(scale, torch.tensor([2.0]))を使う。	Weibullを参照
幾何分布 Geometric （離散：discrete)	Geometric(probs=torch.tensor([0.3])) \(\bullet\) probs=None 0 \(\bullet\) logits=None:tensor	sampleではk+1回目に出るかkを正のintで返す。0の場合は、1回目。 probsかlogitsのどちらかを使用。
超幾何分布 Hyper-Geometric	na	na
ガンマ分布 Gamma （連続：continuous）	Gamma(concentration=torch.tensor([1.0]), rate=torch.tensor([1.0])) \(\bullet\) concentration \(=\alpha =n>0\) \(\bullet\) rate　(=_beta=\mu>0\) 平均発生時間	sampleは事象がn回発生するまでの時間xを返す。 \(rate=1/scale\) concentration \(=\alpha =n>0\):Tensor/float　発生回数 (shape) rate　\(=\beta=\mu>0\):Tensor/float 平均発生時間 concentration, rateの代わりに\(\alpha, \beta\)が使われる事もある。 0
\(\chi^2\)分布 Chi-squared （連続：continuous）	Chi2(df=torch.tensor([1.0])) \(\bullet\) df(=shape):Tensor/float	sampleは事象がn(=df)回発生するまでの時間xを返す。 Gamma(alpha=0.5*df, beta=0.5)と同じ。 df：自由度(degree of freedom) だけ必要。無情報として(1.0)が良く使われる。 0
逆ガンマ分布 Inverse gamma （連続：continuous)	InverseGamma \(\bullet\) concentration \(=\alpha =n>0\)　発生回数 (shape) \(\bullet\) rate　\(=\beta=\mu>0\) 平均発生時間	sampleは出力変数を入力形と同じ形で返す。　共役事前分布の場合は、その出力を正規分布のSigma(=scale)に代入する。
F分布 F distribution (=Fisher-Snedecor) （連続：continuous)	FisherSnedecor(torch.tensor([1.0]), torch.tensor([2.0])) \(\bullet\) df1\(=\phi_1>0\):tensor/float \(\bullet\) df2\(=\phi_1>0\):tensor/float	sampleはxを返す。 log_prob(0
フォンミーゼスフィッシャー分布 Von Mises Fisher (=circular normal) （連続：continuous)	VonMises(loc=torch.tensor([1.0]), scale=torch.tensor([1.0])) \(\bullet\) loc(=\(\mu\)): tensor \(\bullet\) concentration(=\(\kappa>0\)): tensor	sampleは\(-\pi \leq x \leq \pi \)位置を返す。-3.14 \( \leq x \leq \) +3.14 loc(=\(\mu\):　平均、ピークの位置。\(-\pi \leq \mu \leq \pi \) concentration(=\(\kappa\))分布集中度。　大\(\rightarrow\)ピーク鋭くなる。　\(\kappa \sim 0\)の時は一様分布に近づく。 \(-\infty \)log_prob\(\leq \infty\) \(2\pi\)で割った商で循環するので。
ラプラス分布 Laplace （＝二重指数分布、両側指数分布）（連続：continuous)	Laplace(loc=torch.tensor([0.0]), scale=torch.tensor([1.0])) \(\bullet\) loc(=\(\mu\):tensor/float \(\bullet\) scale(=b, diversity):tensor/float	sampleはxを返す。 loc(=\(\mu\):ピーク位置 scale(=b, diversity)：ピークの鋭さ。　小\(\rightarrow\)ピーク鋭くなる。 log_prob(\(-\infty \)x\(\leq \infty\) )
ガンベル分布 Gumbel (=二重指数分布) (=Extreme value Type I) （連続：continuous)	Gumbel(loc=torch.tensor([1.0]), scale=torch.tensor([2.0])) \(\bullet\) loc(=\(\mu\)):tensor:float \(\bullet\) scale(=\(\eta\)):tensor:float	sampleはxを返す。 loc(=\(\mu\):ピーク位置 scale(=\(\eta, \theta\))：ピークの鋭さ。　小\(\rightarrow\)ピーク鋭くなる。 log_prob(\(-\infty
ロジスティック分布 Logistic （連続：continuous)	logistic \(\bullet\) loc(=\(\mu\)):tensor \(\bullet\) scale(=\(\sigma\)):tensor	*PyTorchにはない。TransformedDistributionを使って作らねばならない。（おまけ参照） sampleはxを返す。 loc(=\(\mu\):平均 scale(=\(\sigma \))：標準偏差 log_prob(\(-\infty
パレート分布 Pareto （連続：continuous)	Pareto(torch.tensor([1.0]), torch.tensor([1.0])) \(\bullet\) scale(=\(\beta\))>0:tensor/float \(\bullet\) alpha(=\(\alpha\)=shape)>0:tensor/float	sampleはxを返す。 (注意）\(\beta\)と\(\alpha\)の順番が逆に注意する事。 log_prob(\beta
クマラスワミ分布 Kumaraswamy （連続：continuous)	Kumaraswamy(torch.tensor([1.0]), torch.tensor([1.0])) \(\bullet\) concentration1 (shape):Tensor/float \(\bullet\) concentration0(shape) :Tensor/float	sampleは事象が発生する確率xを返す。 concentration1とconcentration0 はそれぞれ\(alpha, \beta\)で使われる。各事象の発生回数。　出力は各事象の発生確率。 log_prob(0\(\leq\)p\(\leq\)1) log_prob(\(-\infty
安定分布 Stable （＝安定パレート、レヴィ\(\alpha \)分布）	Stable(stability, skew, scale, loc) \(\bullet\) stability:Tensor \(\alpha \in (0,2]\)　小さい程裾野が重い。 \(\bullet\) skew:Tensor \(\beta \in (-1,1]\) \(\bullet\) scale=1 (scale=\(\gamma, \sigma\)):Tensor \(0, \infty\) \(\bullet\) loc=0 (location=\(\delta, \mu_0\)):Tensor \(\bullet\) coord="S0" ("S0"=Nolan's 連続S0パラメータ、"0"=非連続パラメータ）	Levy \(\alpha\)安定分布 mean(),variance()で取り出す。 \(\alpha=2, \beta=0\):　正規分布 \(\alpha=1, \beta=0\):　コーシー分布 \(\alpha=0.5, \beta=0\):　レヴィ分布
無限分解分布 Infinite divisibility(probability)

確率密度分布一覧

分かりにくい確率密度分布をパラメータ違いのグラフで表示。
数値は、あるパラメータの組み合わせの場合の、pyro.sample関数からの出力値50個も表示。

Cauchy分布

loc：中心値
scale：半値半幅

数値＠ loc=0.0, scale=1.0

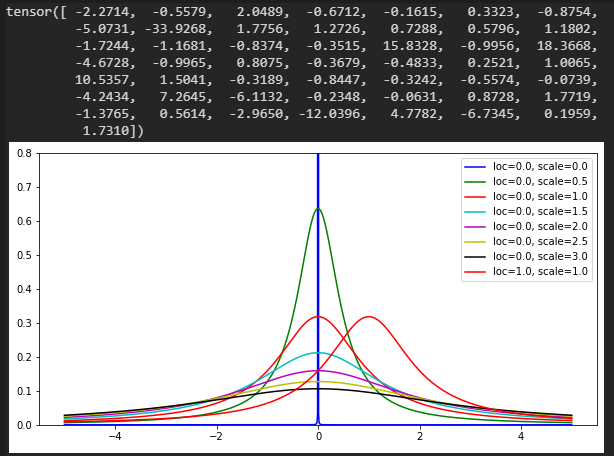
F分布

(Fisher-Snedecor)

df1：自由度１
df2：自由度２

数値＠ df1=5.0, df2=30.0

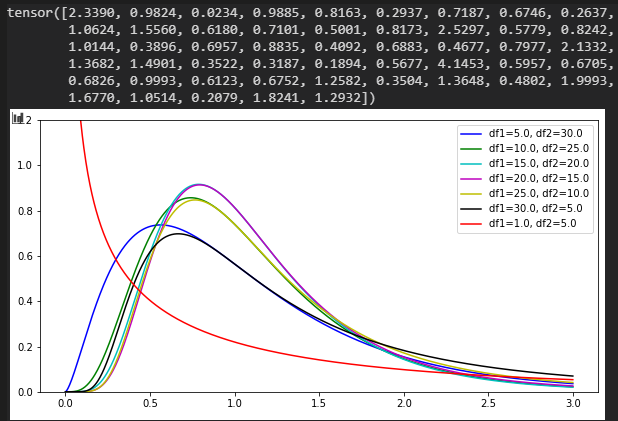
Pareto分布

beta：尺度(scale)
alpha：形状(shape)

数値@beta=1.0, alpha=1.0

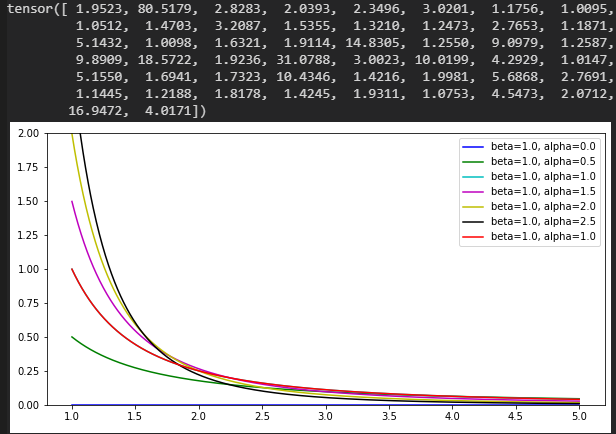
Gumbel分布

loc：ピーク値
scale：バラツキ度

数値＠ loc=1.0, scale=1.0

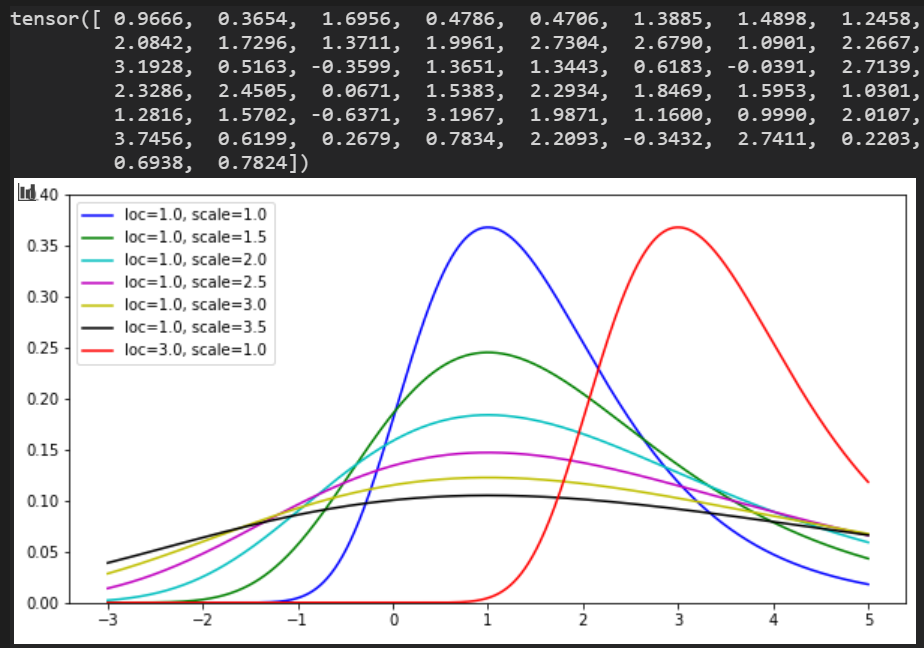
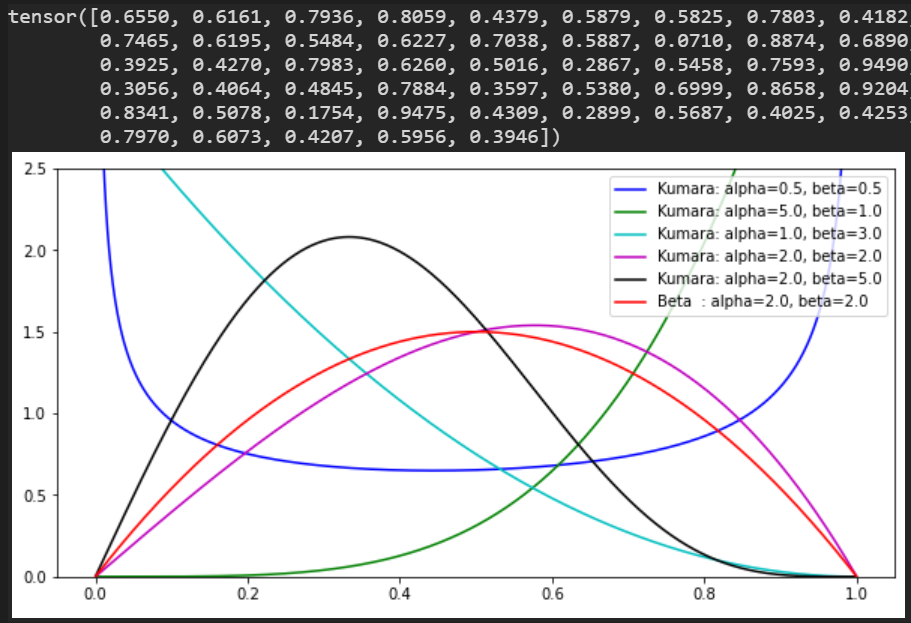
Logistic分布

右グラフは、正規分布とロジスティック分布の違いを表示。　ロジスティックの裾が広いが、loc, scaleによる変化は正規分布と同様。

loc：平均
scale：標準偏差

数値＠ loc=1.0, scale=1.0

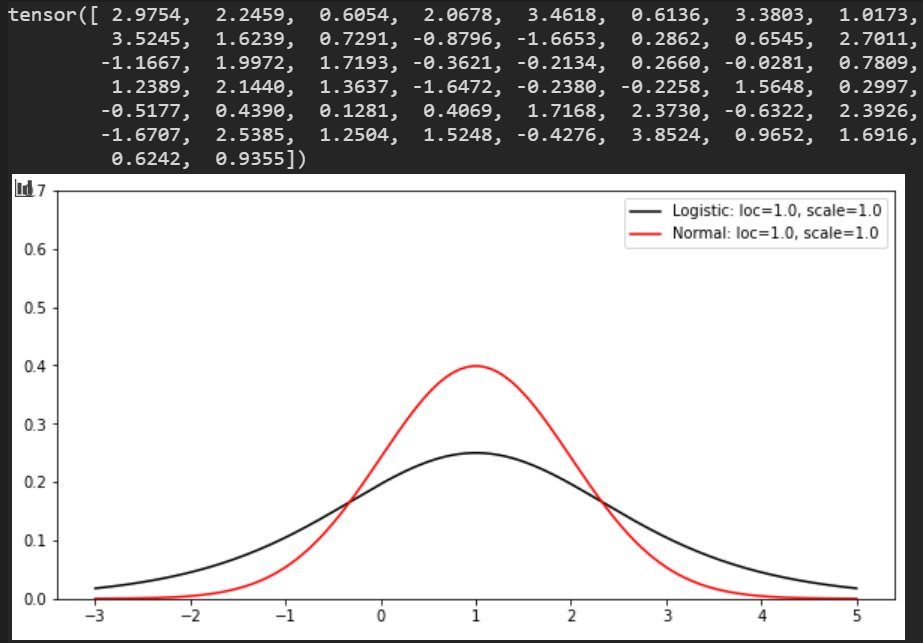
Kumaraswamy分布

右グラフでalpha=beta=2.0の時のベータとの違いも表示。

alpha: 集中度パラメータ
beta: 集中度パラメータ

数値@ 2.0, 2.0

用語

確率密度関数と確率質量関数

Probability Density Function (PDF), Probability Mass Function(PMF)
共に確率変数\(x\)が従う確率密度関数、確率質量関数を\(f(x)\)と表します。

連続型確率分布の関数を、確率密度関数。　離散型確率分布の関数を、確率質量関数。

分布パラメータ (母数＝parameter）

尺度パラメータ(scale parameter) —標準偏差,回数
位置パラメータ(location parameter) —平均
形状パラメータ(shape parameter) —尖り具合、広がり具合
速度パラメータ(rate parameter) —平均発生時間
集中度パラメータ(concentration parameter) —

尤度関数(Likelihood function)と尤度(Likelihood)

ある前提（確率分布/確率関数）で事象が起こる場合に、観察した事象から前提（確率分布/確率関数）が何であったかを推測する時、仮で「もっともらしい関数」として表したものを尤度関数。　尤度関数に観測した事象データを入れて、もっともらしさ加減を算出したものを尤度。　尤度が大きいと尤度関数は前提（確率分布/確率関数）に近いという事になる。　確率（関数）は事象が発生するだろう既知確率であるのに対して、尤度関数は発生（観察）した事象から事象の未知確率関数のもっともらしい関数。

共役事前分布(conjugate prior distribution)

ベイズ推定をする為に、複雑な計算を回避するために考えられた事前分布の事。　データ母集団の確率分布に事前分布をかけると、事後分布が事前分布と同じ関数形になる事前分布の事。　

\(p(\theta|x)\propto p(x|\theta)p(\theta)\)

p(\theta|x)：事後分布（求める分布、予測分布（＝関数）、そして求めた関数から未来を予測。）
p(x|\theta)：尤度[efn_note]Likelihood – もっともらしさ[/efn_note]（観測データに即しているであろう分布の関数を使い観測データのみから求める確率。）
p(\theta)：共役事前分布（尤度の関数形に対応した分布を自分で設定）

共役事前分布 (conjugate prior) \(w(\theta)\)	パラメータ	尤度・尤度関数　\(f(\theta\|z)\) Likelihood	事後分布・予測分布 Posterior distribution
ベータ分布	\(\mu\)	ベルヌーイ分布	ベータ分布（?ベルヌーイ）
ベータ分布	\(\mu\)	二項分布	ベータ分布（？＋二項分布？）
ディリクレ分布	\(\pi\)	多項分布	ディリクレ分布（？＋多項分布？）
正規分布（ガウス）	\(\mu\)	正規分布（ガウス）(\(\sigma^2\)既知、平均未知)	正規分布（ガウス）
逆ガンマ分布＝＞GelmanによるとUniformを使う事を奨励している。　Pyroでも使用できた。	\(\lambda\)???	正規分布（ガウス）(\(\sigma^2\)未知、平均既知	逆ガンマ分布
ガンマ分布	\(\lambda\)	正規分布（ガウス）？？？	t分布
多変量正規分布（多次元ガウス）（共分散固定）平均を求める	\(\mu\)	多変量正規分布（多次元ガウス）平均未知、分散既知	正規分布（ガウス）
逆Wishart分布（平均固定）共分散を求める	\(\Lambda\)	多変量正規分布（多次元ガウス）平均既知、分散未知	多次元t
ガンマ分布	\(\lambda\)	ポアソン分布	ガンマ分布（負の二項分布？）
ディリクレ分布	\(\pi\)	カテゴリ分布	カテゴリ分布
ガンマ分布	\(\displaystyle \frac{1}{\lambda}, \frac{1}{\lambda^2}\)	指数分布	ガンマ分布

特性関数(characteristic function)

ある確率変数の分布の特性を示す関数。その確率密度関数と累積分布関数の両方を完全に定義する関数。分布のフーリエ変換と同じ。　特徴関数や定義関数とも言われる。　確率変数の重み付きの和の分布や確率分布列の収束の証明にも利用される。

\(\phi(t) \equiv E[e^{itX}]=\int e^{itx}dF(x)\)　　\(t\)は実数パラメータ, \(i\)は虚数単位

母関数(generating function)

関数\(g(\xi)\)のべき級数展開の係数の数列\(a_n\)や関数列\(a_n(z)\)がある時、この\(g(\xi)\)を\(a_n\)や\(a_n(z)\)の母関数という。

\(\displaystyle g(\xi)=\sum_{n \to 1}^{\infty} a_n(z) \xi^n\), \(\displaystyle g(\xi)=\sum_{n \to 1}^{\infty} a_n \xi^n\)

下の形は数列\(a_n\)の母関数として扱われ、指数的母関数(exponential general function)と言う事がある。

\(\displaystyle g(\xi)=\sum_{n \to 1}^{\infty} \frac{a_n}{n!} \xi^n\)

モーメント（=積率）

モーメントは平均や分散等の一般化したもの。
モーメントはどんな風にデータがバラバラになっているかを表す情報。
モーメントはモーメント（＝原点からのモーメント）と　中心モーメント（＝平均まわりのモーメント）の２種類がある。
モーメント（＝原点からのモーメント） \(\mu_k’=E[X^k]\)
確率の和は、0次のモーメント（＝原点からのモーメント） \(\mu_k=E[(X-E[X])^k]\)
平均は、1次のモーメント（＝原点からのモーメント）
分散は、2次の中心モーメント（＝平均まわりのモーメント）
歪度は、3次の中心モーメント（＝平均まわりのモーメント）
尖度は、４次のモーメント（＝原点からのモーメント）
モーメント離散型\(E[(x-a)^k]\)、連続型\(\displaystyle E[(x-a)^k]=\int_{-\infty}^{\infty}(x-a)^kf(x)dx\)

積率(=モーメント）

正の整数である\(k\)あるとき、\(E[X^k]\)を確率変数\(X\)の\(k\)次積率(k-th moment)という。
また\(\mu=E[X]\)としたとき、\(E[(X-\mu)^k]\)を\(k\)次の中心積率(k-th central moment)や平均回りの\(k\)次の積率と言う。

原点回りの積率の場合、\(\mu=0\)となる。

平均回りの1次の積率は常に０。　\(E[X-E[X]]=0\)

確率・オッズ・ロジット

確率\(p\)に対してオッズ\(odds\)とロジット\(logit\)は以下の様になる。

\(\displaystyle odds(p)=\frac{p}{1-p}\)　賭け率、勝率

\(\displaystyle Logit(p)=\log_e \left(\frac{p}{1-p}\right)\)

\(x_i\)の観測データから、最尤法によって\(a,b\)を推定して、成功確率を推定したりする。

\(\displaystyle Logit(p_i)=a+bx_i\)

ロジットの逆関数はSigmoid曲線となる。

\(\displaystyle p=\frac{1}{1-e^{-logit(p)}}, \quad f(x)=\frac{1}{1-e^{-x}}\)

モーメント母関数(moment generating function)

あらゆる次数のモーメントをにおける関数。
\(t\)は次数。　0（＝0次モーメント）を入れると必ず１になる。（確率の和は全て足すと１になる。）

\(\displaystyle E[e^{tX}]=\sum_{t \to 0}^{n}e^{tx_i}p_i=\int_{-\infty}^{\infty}e^{tx}f(x)dx \qquad \) (但し、\(t \in \mathbb{R}\))

ガンマ関数

\(\displaystyle \Gamma(\frac{n}{2})=\int_0^{\infty}t^{\frac{t}{2}-1}e^{-t}dt\qquad\) (\(n\)：自由度)

ベータ関数

連続

\(\displaystyle B(p,q)=\int_0^1y^{p-1}(1-y)^{q-1}dy=\frac{\Gamma(p)\Gamma(q)}{\Gamma(p+q)}\)

離散

\(\displaystyle\ \frac{1}{B(n,m)}=\frac{(m+n-1)!}{(m-1)!(n-1)!}=\frac{{}_{m+n-1}P_{m-1}}{(m-1)}=\frac{{}_{m+n-1}P_{n-1}}{(n-1)}={}_{m+n-1}C_{m-1}={}_{m+n-1}C_{n-1}\)

GMM（Gaussian Mixture Model）混合ガウシアンモデル

複数のガウス分布（＝正規分布）が重なったモデルの事。

\(\displaystyle p(x)=\sum_{k \to 1}{K} \pi_kN(x|\mu_k, \sigma_k)\)

歪度(skewness)、尖度(kurtosis)

歪度は分布のピークが中央の時、０。　左側の場合、正の値。　右側の場合、負の値となり、歪み度合を表すもの。　歪度が存在しない分布もある。

歪度＝\(\displaystyle \frac{E[(X-\mu)^3]}{\sigma^3}\)　

尖度は、平均近傍に分布が集中し、そして裾が重くなる事を表す。

尖度：\(\displaystyle \frac{E[(X-\mu)^4]}{\sigma^4}-3\)　

おまけ：ロジスティック分布作り方

loc=torch.tensor([1.0])
scale=torch.tensor([1.0])
transforms = [dist.transforms.SigmoidTransform().inv, dist.transforms.AffineTransform(loc=loc, scale=scale)]
logistic = dist.TransformedDistribution(base_distribution, transforms)
y=[logistic.log_prob(torch.tensor([x])).exp().to('cpu').detach().numpy().copy() for x in x_range]
plt.plot(x_range, y, c='r', label=f'Normal: loc={loc[0].numpy():.1f}, scale={scale[0].numpy():.1f}')
ye=pyro.sample('ye',logistic)

おまけ：英語

自由度：df = degree of freedom
台：support

おまけ：カイ二乗検定

ベイズ推定等とは異なる。

独立性のカイ二乗検定(chi-square test)　(=ピアソンのカイ二乗検定)

２つの変数が独立か関連があるかを判定する事。　分割表の各セルの（期待度数ー観測値\()^2\)がカイ二乗分布に近似できる。　データが少ない時はフィッシャーの正確確率検定を行う。

各セルの期待度数：　\(\displaystyle E_{ij}=Np_ip_j=\frac{n_{i.}n{.j}}{N}\)

カイ二乗に従った期待値とのずれ総和：　　 \(\displaystyle \chi^2=\sum_{i=1}^r\sum_{j=1}^c\frac{(n_{ij}-E_{ij})^2}{E_{ij}}\)

各セルの期待度数を計算(\(E_{ij}\)式)
期待度数とのずれ総和を計算(\(\chi^2\)式)
自由度(r-1)(c-1)を算出
自由度と２のずれ総和からカイ二乗分布表を使いあり得る確率（P値）を算出
あり得る確率（P値）が0.05以下（あり得る確率が5%以下）なら帰無仮説を棄却（＝独立でない）

適合検定(goodness of fit test)

帰無仮説における期待度と実際の観測データの当てはまり良さを検定する事。

分布名 Distribution name	式 Equation	概要 Remarks
連続型一様分布 continuous uniform （連続:continuous)	\(\displaystyle f(x\|a,b) =\frac{1}{b-a} \qquad \) \( \qquad (a\leq x\leq b) \\ =0 \qquad (x < a, x>b)\) \(\displaystyle E[X]= \frac{a+b}{2}\\ \displaystyle V[X]=\frac{(b-a)^2}{12}\)	完全にランダムな事象の場合。 Uniform(\(-\infty,\infty\))はimproperな事前分布。グループ数が小さい場合、一様分布は事後分布への影響大。　（ー＞HalfCauchy分布を使う。） Uniform(0､b)として大きなbを使う。弱情報事前分布の場合、考えられる分散（弱情報）をbに入れておくる。
ベルヌーイ分布 Bernoulli （離散:dicrete)	\(\displaystyle f(x;p)=p^x(1-p)^{}1-x \\ \qquad(x \in(1,0))\) \(\mu=p, \sigma^2=p(1-p)\)	二項分布で回数が1回か０回しかない場合の分布。　試行を２回以上の場合は二項分布。共役事前分布はベータ分布。
二項分布 Binomial （離散:dicrete）	\(f(k\|p,N)={}_N \mathrm{C}_kP^N(1-p)^{N-k}\) \(E[X]=Np \\ V[X]=Np(1-p)\) \(\phi(t)=(1-p+pe~{it})^N\)	成功か失敗しかない試行をN回繰返し、k回成功する確率。視聴率の推定。（二項分布->正規近似）共役事前分布はベータ分布。
負の二項分布 negative binomial （離散：discrete)	\(\displaystyle f(k\|r,p) =\begin{pmatrix} k+r-1 \\ k \end{pmatrix}(1-p)^rp^k \) \(\displaystyle E[X]=\frac{pr}{1-p}\\ \displaystyle V[X]=\frac{pr}{(1-p)^2}\)	平均発生数が一定と仮定できない(ポアソン分布が適しない)計数推定に利用できる。 r 回の失敗までに k 回の成功が起こる確率。無限分解分布
多項分布 Multinomial （離散:dicrete）	\(\displaystyle f(m\|\mu,N)\) \(\displaystyle=\frac{N!}{m_1!, \cdots , m_K!}p_1^{m_1}\) \( \qquad \displaystyle \cdots p_K^{m_K} \frac{N!}{m_1!, \cdots , m_K!}\prod_{i \to 1}^K \mu_i^{m_i} \)	複数(N回)試行する二項（成功か失敗）の項目を1~6の様に３以上の多項（K>2）の分布。 \(m_i\)は\(i\)の項目が出た回数。　\(p_i\)は\(i\)が出る確率。　出た順番は関係ない。 \(\sum_{k=1}^k \mu_k=\sum_{k=1}^k p_k=1\) N=1の多項分布がカテゴリカル分布。共役事前分布はディリクレ分布。
カテゴリカル分布 Categorical （離散:dicrete）	\(\displaystyle f(m\|\mu,K)\\=p_1^{m_1} \cdots p_K^{m_K} \\ \displaystyle =\prod_{i \to 1}^K \mu_i^{m_i} \)	多項分布で試行回数がN=1の場合がカテゴリカル分布。またカテゴリカル分布のK=2とするとベルヌーイ分布。 \(\sum_{i=1}^K \mu_i=1\) 共役事前分布はディリクレ分布。
ディリクレ分布 Dirichlet (=多変量ベータ分布）（連続:continuous)	\(\displaystyle f(\mu_i\|\alpha_i) \\ \displaystyle =\frac{1}{B(\alpha)}\prod_{i=1}^{N} \mu_i^{\alpha_i-1} \) \(\displaystyle B(\alpha)=\frac{\prod_{i=1}^N\Gamma(\alpha_i)}{\Gamma(\sum_{i=1}^{N}\alpha_i)}=C\) (定数）	ベータ分布の多変量な場合。（多変量ベータ分布とも呼ばれる） N個の事象がそれぞれ\(\alpha_i-1\)回発生した時の確率\(\mu_i\)を求める。多項分布（二項分布@N=2）の共役事前分布。混合モデルに使われる。条件\(\sum_{i \to 1}^N \mu_i^{\alpha_{i-1}}=1, \alpha_i \in \mathbb{R}>0\)
ベータ分布(１種） Beta distribution of the first kind （連続:continuous)	\(\displaystyle f(p\|\alpha,\beta) \\=\displaystyle \frac{p^{\alpha-1}(1-p)^{\beta-1}}{B(\alpha, \beta)} \\ \quad (0 \leq p\leq1)\) ベータ関数\(\displaystyle B(\alpha,\beta) =\frac{\Gamma (\alpha) \Gamma (\beta)}{\Gamma(\alpha+\beta)}\) \(\displaystyle E[X]=\frac{\alpha}{\alpha+\beta} \\ \displaystyle V[X]=\frac{\alpha\beta}{(\alpha+\beta)^2(\alpha+\beta+1)}\)	ディリクレ分布のN=2。ベイズ統計でよく使われる。\(\alpha\)は事象発生回数、\(\beta\)は発生しなかった回数。両方とも、形状(shape)母数。固定された範囲を上回る可能性を表す場合。[efn_note]これが\(\displaystyle \int_{-\infty}^{\infty} \frac{(x-\mu)^2}{\sigma^2}dx\)[/efn_note] 二項分布のprobsに与える共役事前分布。 Beta(0.5,0.5)はJeffreys事前分布。（無情報事前分布？） Beta(0,0)はimproperな事前分布。
正規分布 Normal （=ガウス分布：Gaussian）（連続: continuous)	\(\displaystyle f(x\|\mu,\sigma^2)\\=\displaystyle \frac{1}{\sqrt{2 \pi \sigma^2}}\exp\left(-\frac{(x-\mu)^2}{2\sigma^2}\right)\)	ランダムノイズ、中心極限定理カーネル密度推定 Normal(\(\mu,\sigma\)) 無限分解可能分布
多変量正規分布 Multivariate Normal （連続: continuous)	\(\displaystyle X ~\mathcal{N}_k(\mu_i, \Sigma_{ii})\) \(\displaystyle \mu=E[X]=(E[X_1],\cdots,E[X_k]\) \(\displaystyle \sum_{i,j}:=Cov[X_i,X_j]=E[(X_i-\mu_i)(X_j-\mu_j)]\)	混合ガウシアンでよく使う。分散共分散逆行列は精度行列(precision matrix)、\(Q=\Sigma^{-1}\)
対数正規分布 Log-normal （連続: continuous)	\(\displaystyle f(x\|\mu,\sigma^2)\\=\displaystyle \frac{1}{\sqrt{2 \pi \sigma^2}}\exp\left(-\frac{(\log x-\mu)^2}{2\sigma^2}\right)\) \(\displaystyle E[X]=\exp(\mu+\frac{\sigma^2}{2}) \\ V[X]=\exp(2\mu+\sigma^2)(\exp(\sigma^2)-1)\)	各人が保有する資産の分布に近い。株価 LogNormal(\(\mu,\sigma\))
t分布 Student's t （連続: continuous)	\(\displaystyle f(x\|n)=\frac{\displaystyle \Gamma(\frac{n+1}{2})}{\displaystyle \sqrt{n \pi} \, \Gamma(\frac{n}{2})}(1+ \frac{x^2}{n})^{-(\frac{n+1}{2})}\)	正規分布の試行数n（自由度）が少ない場合。正規分布の山が低く、すそ野が広がったグラフ。n\(\rightarrow \infty\)で正規分布に一致する。 t分布表。　平均は0。　分散当たりの%点は自由度により異なる。無限分解可能分布
多変量t分布 Multivariate student's t （連続: continuous)	\(f(x_i\|p,n,\mu_i,\Sigma_{ii}) \) \( =\displaystyle \frac{\displaystyle \Gamma(\frac{n+p}{2})}{(\sqrt{n \pi})^p\Gamma(\frac{n}{2})\|\Sigma\|^{\frac{1}{2}}}\) \( \displaystyle \qquad \times \left[1+\frac{1}{n}(x-\mu)^{\top} \Sigma^{-1}(x-\mu) \right]^{\displaystyle -\frac{(n+p)}{2}}\)	ランダムp次元ベクトルのt分布。 n:自由度　（n=1 \(\rightarrow \)多変量コーシー分布） \(x\): (p x 1)ベクトル \(\mu\):平均　(p x 1)ベクトル \(\Sigma\):\(\sigma\)のp x p行列としての記号。 \((x-\mu)^{\top\}): 縦ベクトルへの転置。
コーシー分布 Cauchy (＝ローレンツ分布） (＝ブライト・ワグナー分布（物理））（連続：continuous)	\(\displaystyle f(x\|\mu,\gamma)=\frac{1}{\pi \gamma \left\{1+\left(\frac{x-\mu}{\gamma}\right)^2 \right\}}\) \(\mu=0, \gamma=1\)の時、標準コーシー分布。期待値、分散が存在しない。	自由度1のt分布が標準コーシー分布。　期待値が存在しない。（大数の法則が成立しない）　裾が厚い分布の代表。(外れ値を取る確率が低い。）証券価格の大暴落などの滅多に起こらない事象をモデル化する場合など）正の範囲だけー＞半コーシー分布。グループ数が少ない時、階層分散パラメータの条件付共役事前分布。 \(\sigma_{\alpha}=0\)で最大値となり、なだらかに減少。 \(x\)が小さいとピークも低くすそ野が広がる。強制共鳴や分光学の共鳴広がり等スペクトル線形状。無限分解可能分布、安定分布 \(\mu\) location parameter 最頻値 \(\gamma\) scale parameter 半値半幅
ポアソン分布 Poisson （離散：discrete)	\(\displaystyle f(k\|\lambda)=e^{-\lambda} \frac{\lambda^k}{k!}\) \(E[X]= V[X]=\lambda\)	レアでランダムな事象が単位時間に\(\lambda\)数発生する場合の確率分布。　\(k\)：発生数交通事故の回数。　不良品の割合。病気に疾患する確率。二項分布と比べ、n->大、p->小さい、np=一定\((\lambda)\) 二項分布の近似で機械学習での計算が楽になる。無限分解可能分布
指数分布 exponential （連続: continuous)	\(\displaystyle f(t\|\mu)=\frac{1}{\mu}e^{-\frac{t}{\mu}}\\ =\lambda e^{-\lambda x}\\ \quad (t \leq 0)\) \(\displaystyle E[X]=\mu = \frac{1}{\lambda} \\ \displaystyle V[X]=\mu^2=\frac{1}{\lambda^2}\)	ランダムな事象の発生の平均時間間隔\(\mu\)の時、次に起こるまでの期間\(t\)の確率密度分布。機械故障間隔（MTBF)。　客到着間隔。実際確率を出すには、確率密度を経過時間（区間）で積分すると確率になる。 \(\displaystyle \lambda=\frac{1}{\mu}\)：単位時間内での発生回数。幾何分布の連続型。似ているが、ポアソン分布は離散型で、単位時間に\(\lambda\)回起こる現象がX回起こる確率分布で、時間経過を出すものでない。　指数分布＝＞期間　ポアソン分布＝＞回数
ワイブル分布 Weibull （＝最弱Ringモデル）（連続：continuous)	\(\displaystyle f(t\|\eta,m)\\ \displaystyle =\frac{m}{\eta}\left( \frac{t}{\eta}\right)^{m-1}\exp\left\{ -\left( \frac{t}{\eta}\right)^m\right\}\) \(\qquad (0 \text{<}x )\)	物体の強度を統計的に記述する為の分布。バスタブ曲線の様に、時間に対する劣化現象や寿命の場合。 \(\eta\): 尺度(scale)：発生平均時間の様なもの。--分布のピーク。 m:ワイブル係数（形状母数:shape)--分布のバラツキ。 m=1：指数分布ｍ=2：レイリー分布 m\(\rightarrow　\infty\)：正規分布 m<1:初期故障 m=1：偶発故障故障率のヒストグラムを作り、ワイブル確率子にプロットしmを読み取る。 m>1:摩耗・劣化故障
レイリー分布 Reyleigh （連続：continuous)	\(\displaystyle f(x\|\sigma^2)=\frac{x}{\sigma^2}e^{-\frac{x^2}{2\sigma^2}}\) \(\displaystyle E(x)=\sigma\sqrt{\frac{\pi}{2}} \\ \displaystyle V[X]=\left(2-\frac{\pi}{2}\right)\sigma^2\)	風力発電量予測、マイクロ波無線通信、移動無線通信の伝搬解析、超音波診断自由度２のワイブル乗分布
幾何分布 Geometric （離散：discrete)	\(\displaystyle f(k\|p)=p(1-p)^{k}\) \(\displaystyle E[X]=\frac{1}{p} \\ \displaystyle V[X]=\frac{1-p}{p^2}\)	既知な成功確率で、試行k+1回数内で成功する確率を求める場合。 p：成功率『離散的な待ち時間分布』無限分解分布
超幾何分布 Hyper-Geometric	\(\displaystyle P(X=x)=\frac{{}_M \mathrm{C}_{x} \cdot {}_{N-M} \mathrm{C}_{n-x}}{{}_N \mathrm{C}_n}\) \(\displaystyle E[X]=\frac{KM}{N} \\ V[X]=\frac{K(N-K) \frac{M}{N}(1-\frac{M}{N})}{N-1}\)	当たりM個、外れN-M個のボール。　Kを取り出した時、当たりX個となる確率。既知の不良率で抜き取った標本の不適合個数の分散。薬（あり・なし）で発症を抑えたかどうか（発症・なし）を見る臨床実験。
ガンマ分布 Gamma （連続：continuous）	\(\displaystyle f(x\|n,\mu) =\frac{1}{ \mu^n　\Gamma(n)} x^{n-1} e^{-\frac{x}{\mu}}\\ \quad (0 \leq x)\) \(\displaystyle E[X]=n\mu\)：n回発生する平均時間 \( V[X]=n\mu^2\)：n回発生する時間分散	期間\(\mu\)内に１回起こるランダムな事象がｎ回起こるまでの時間の分布。指数分布に回数(n)を使えるよう一般化したものなので、指数分布と考え方は同じ。 \(x\)は時間。　\(f(x)\)はある時間の時に起こる確率 10年に1回起こる事象が２回起こるまでの年数。　電子部品の寿命分布。　通信トラフィック待ち時間。　所得分布。　ウィルスの潜伏期間。『連続的な待ち時間分布』無限分解可能分布 n=1の時が指数分布。　nを極大化すると正規分布。 n: 発生回数 \(=\alpha\) shape parameter \(\mu\):平均発生時間 \(=\beta\) 　scale parameter \(\lambda=\frac{1}{\mu}\): 単位時間発生回数 rate parameter
\(\chi^2\)分布 Chi-squared （連続：continuous）	\(\displaystyle Z \sim\chi_n^2 =f(x\|n)=\displaystyle \frac{1}{2^{\frac{n}{2}} \Gamma (\frac{n}{2} ) }x^{\frac{n}{2}-1}e^{-\frac{x}{2}} \\ \quad (0 < x)\)	独立に標準正規分布に従う k 個の確率変数 \(X_1,\cdots, X_n\) をとる時、\(Z=\sum_{i \to 1}^nX_i^2\)の事を自由度nのカイ二乗分布。ガンマ分布の\(n \to \frac{n}{2},\mu \to 2\)の場合がカイ二乗分布。カイ二乗検定やフリードマン検定等、推計統計学で多用される。　自由度\(n\)が大きくなると正規分布に近づく。カイ二乗分布表。カイ二乗分布の多次元はウィシャート分布。
逆ガンマ分布 Inverse gamma （連続：continuous)	\(\displaystyle f(x\|n,\mu)=\frac{\mu^n}{ \Gamma(n)} x^{-n-1} e^{-\frac{\mu}{x}}\\ \quad (0 \leq x)\) \(\displaystyle \Gamma(\alpha)=\int_0^{\infty}x^{-\alpha-1}e^{-\frac{\beta}{x}}\) \(\displaystyle E[X]=n\mu \\ V[X]=n\mu^2\)	正規分布の分散が不明の時の共役事前分布。 InvGamma(\(x_i,y_i\)) n: 発生回数 \(=\alpha\) 形状(shape) パラメータ \(\mu\):平均発生時間 \(=\beta\)　尺度(scale)パラメータ \(x\):単位時間当たりの発生回数 \(ｇ(x\|n,\mu)\)は、平均発生時間\(\mu\)の事象が、n回発生する確率密度分布で、単位時間当たりに\(x\)回発生する確率を表す関数。 (＊Andrew Gelmanによると階層分散パラメータの事前分布として使うべきでない？） InverseGamma(0,0)はimproperな事前分布。逆ガンマ分布の多次元が逆ウィシャート分布。
F分布 F distribution (=Fisher-Snedecor) （連続：continuous)	\(\displaystyle F(x\|\phi_1,\phi_2)=\frac{\displaystyle \frac{\phi_1}{\phi_2}^{\frac{\phi_1}{2}}}{\displaystyle B(\frac{\phi_1}{2},\frac{\phi_2}{2})} \frac{\displaystyle x^{\frac{\phi_1}{2}-1}}{\displaystyle (1+ \frac{\phi_1}{\phi_2}x)^{\frac{\phi_1+\phi_2}{2}}}\) \(\displaystyle F=\frac{\displaystyle \frac{\chi_1^2}{\phi_1}}{\displaystyle \frac{\chi_2^2}{\phi_2}}\)	\(F\)分布は自由度\(\phi_1. \phi_2\)であるカイ二乗分布\(\chi_1^2, \chi_2^2\)が独立の時の比。仮説検定の時よく使う。 \(\bullet\: F(1,\phi_2)=\{t(\phi_2)\}^2\) \(\bullet\: F(1,\infty)=\{t(\infty)\}^2=Z^2,Z\sim N(0,1)\) \(\bullet\: F(\phi_1,\infty)\rightarrow \chi^2(\phi_1)\) \(\bullet\: F(\infty,\infty)\rightarrow\chi^2(\infty)\sim\)　正規分布
フォンミーゼスフィッシャー分布 Von Mises Fisher (=circular normal) （連続：continuous)	\(\displaystyle f(x\|\mu,\kappa)\\ \displaystyle=\frac{e^{\kappa \cos(x-\mu)}}{2\pi I_0(\kappa)}\\=Ce^{\kappa \mu^{\top} x }\)	方向データに対する球面上における確率分布。 \(\|x\|=1\): 単位球面上、長さ１のベクトル。\(-\pi \leq x \leq \pi\) 平均方向(位置(location)パラメータ)：\(-\pi \leq \mu \leq \pi\) 集中度(形状(shape)パラメータ）：\(\kappa>0\) 大きくなるとピークが鋭くなる。　小さくなると裾が厚くなる。　0に近づくと一様に近づく。 \(C\)は定数。
ラプラス分布 Laplace （＝二重指数分布、両側指数分布）（連続：continuous)	\(\displaystyle f(x\|\mu,b)=\frac{1}{2b}\exp(-\frac{\|x-\mu\|}{b})\) \(\displaystyle E[X]=\mu \\ V[X]=2b^2\)	正規分布の中心を高くして、すそ野を広げた感じ。左右対称。音源・機密保護などに使われる。 bが小さい程ピークが高くなり、鋭くなる。bがほぼ0で、ピーク以外の確率密度は0になる。 \(\mu\)はピーク位置。位置(location)パラメータ
ガンベル分布 Gumbel (=二重指数分布) (=Extreme value Type I) （連続：continuous)	\(\displaystyle f(x\|\mu,\eta)\) \( \displaystyle=\frac{1}{\eta}\exp\left\{-\left(\frac{x-\mu}{\eta} \right)\right\}\exp\left[-\exp\left\{-\left(\frac{x-\mu}{\eta}\right)\right\}\right]\)	極値分布のタイプI。極値統計滅多に起こらない事象（洪水、台風、干ばつ等）右裾が厚くなる分布。 \(\mu\)位置(location)パラメータ \(\eta\) 尺度(scale)パラメータ
ロジスティック分布 Logistic （連続：continuous)	\(\displaystyle f(x\|\mu,\sigma) =\frac{\exp(-\frac{x-\mu}{\sigma})}{\sigma \left[1+\exp(-\frac{x-\mu}{\sigma})\right]^2}\)	正規分布と酷似していて左右対称。　ロジスティック分布の方が裾が長い。 \(\mu\) 位置 (location)パラメータ \(\sigma\) 尺度(scale)パラメータ
パレート分布 Pareto （連続：continuous)	\(\displaystyle f(x\|\alpha, \beta)=\frac{\alpha/\beta}{(x/\beta)^{\alpha+1}}\) \(\displaystyle E[X]=\frac{\alpha \beta}{\alpha-1}\quad(\alpha>1) \) \( \displaystyle V[X]=\frac{\alpha\beta^2}{(\alpha-1)^2(\alpha-2)} \quad (\alpha>2)\)	所得の分布をモデリングする分布。　離散型はゼータ分布。 \(\alpha\)形状(shape)パラメータ \(\beta\):尺度(scale)パラメータ
クマラスワミ分布 Kumaraswamy （連続：continuous)	\(f(x\|\alpha,\beta)=\alpha\beta x^{\alpha-1}(1-x^\alpha)^{\beta-1}\) \(0\leq x \leq 1\) \(\alpha>0, \beta>0\)	ベータ分布に類似だがもっと簡単。 \(\alpha,\beta\):形状(shape)パラメータ \(\alpha=1\)か\(\beta=1\)の時、ベータ分布と同じ。 Kuma(\(\alpha\),1)=Beta(\(\alpha\),1)
安定分布 Stable （＝安定パレート、レヴィ\(\alpha \)分布）	確率密度は特性関数を用いてしか表せれない。 \(\displaystyle f(x)=\frac{1}{2 \pi} \int_{-\infty}^{\infty} \varphi(t)e^{-ixt}dt\) 条件 \(S_n=\frac{1}{\alpha_n}\sum_{i=1}^n X_i-\beta_n \)	正規分布やコーシー分布を含む広い概念。　しかし、Pyroでは正規分布より裾野が重い分布を指しており、外れ値が多く、正規分布では精度がでにくい場合に正規分布に変わってStable分布を使う。パラメータは４つ（母数） \(\alpha\): 　裾野の重さを表す。　小さい程、すそ野が重い。 \(\beta\): 　歪を表す。　０の時、左右対称。 \(\alpha\):　規模を表す。 \(\alpha\):　平行移動。全ての\(\beta_n=0\)の時、厳密に安定（strictly stable)。
無限分解分布 Infinite divisibility(probability)	確率変数\(x_{n1},x_{n2}, \cdots , x_{nn}\)が\(F\)の分布の時、 \(Sn(=x_{n1}+x_{n2}+ \cdots + x_{nn})\)が同じ\(F\)分布となる時、\(F\)分布は無限分解分布。	任意の数の独立した同一分布の（i.i.d.）確率変数の合計の確率分布の種類の総称。　連続型では、正規分布、コーシー分布、t分布、ガンマ分布。離散型では、ポアソン分布、負の二項分布、幾何分布等。一様分布や二項分布は無限分解分布でない。それぞれの無限分解可能分布はレヴィ過程に対応している。

数学　分布　まとめ　（一覧表、Pyro関数、用語など）

分布一覧（式、意味）

分布一覧（Pyro 関数・引数・sample出力メモ）